負の数の基礎
絶対値
答えが負の数になる引き算
負の数を足す
負の数を引く
負の数を掛ける
負の数で割る
負の指数
「算数・数学」の部屋に戻る
ここでは、主に整数について説明しますが、小数、分数その他についても同様に考えられます。
1,2,3・・・のように0より大きい数を「正の数」といいます。
それに対して、0より小さい数を「負の数」といい、正の数に「負号(−):マイナスと読む」をつけて
−1,−2,−3・・・のように表します。
−1は0より1小さい数、−2は0より2小さい数です。
正の数は、ものの個数を数えることによりその計算を理解することができますが、
負の数は0より小さい数として作り出された数ですので、その計算も、それまで
正の数でおこなっていた計算の規則が崩れないように、作り出す必要があります。
絶対値
負の数(例えば −3)の負号を取り除いた数(3)を、もとの数の絶対値と言います。
正の数および 0 は、その数自身が絶対値です。
※例:絶対値が7になる数は、7 と −7 の2つあります。
答えが負の数になる引き算
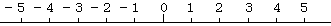
上のような数直線において、
足し算の例:3+2 3 から 2 だけ右に移動した位置。答えは 5。
引き算の例:3−2 3 から 2 だけ左に移動した位置。答えは 1。
のように、足し算、引き算の方法を決めることができます。
これを利用して、引かれる数よりも大きい数を引くことができます。
例: 2−5 2 から 5 だけ左に移動した位置。答えは
−3。
4−6 4 から 6 だけ左に移動した位置。答えは
−2。
このような計算をいろいろやっていくと、次のようなことが分かります。
| a から、それよりも大きい数 b を引くには、b−a
を計算して、そのあとに負号(−)を付ければよい。 |
ほかにも、
−4−3・・・(負の数からさらに引く)
−4+7・・・(負の数に正の数を足す:答えが正の数になる場合)
−4+3・・・(負の数に正の数を足す:答えが負の数になる場合)
についても、計算できるようにしてください。
上へ
負の数を足す
3+3=6
3+2=5
3+1=4
3+0=3
このように、足す数を1ずつ減らすと、答えも1ずつ減ります。
この規則を崩さないように、さらに足す数を減らすと、
3+(−1)=2
3+(−2)=1
3+(−3)=0
3+(−4)=−1
のように、負の数を足すことができます。
このような計算をいろいろやっていくと、次のようなことが分かります。
| ある負の数を足すことは、その数の絶対値を引くことと同じである |
上へ
負の数を引く
3−3=0
3−2=1
3−1=2
3−0=3
このように、引く数を1ずつ減らすと、答えは1ずつ増えます。
この規則を崩さないように、さらに引く数を減らすと、
3−(−1)=4
3−(−2)=5
3−(−3)=6
3−(−4)=7
のように、負の数を引くことができます。
このような計算をいろいろやっていくと、次のようなことが分かります。
| ある負の数を引くことは、その数の絶対値を足すことと同じである |
上へ
負の数を掛ける
(正の数)×(負の数)
3にいろんな数を掛けてみます。
3×4=12
3×3=9
3×2=6
このように、掛ける数を1ずつ減らすと、答えは3ずつ減ります。
この規則を崩さないように、さらに掛ける数を減らすと、
3×1=3
3×0=0
のように、1を掛ける、0を掛けるということもできますし、さらに
3×(−1)=−3
3×(−2)=−6
3×(−3)=−9
3×(−4)=−12
のように、負の数を掛けることもできます。
さらに、「掛け算は掛けられる数と掛ける数を交換しても答えは変わらない」(交換法則といいます)
という性質から、(負の数)×(正の数)も計算できます。
このような計算をいろいろやっていくと、次のようなことが分かります。
(正の数)×(負の数)または(負の数)×(正の数)の計算は、
絶対値どうしの掛け算の答えに、負号を付ければよい。 |
(負の数)×(負の数)
−3にいろんな数を掛けてみます。
−3×3=−9
−3×2=−6
−3×1=−3
−3×0=0
このように、掛ける数を1ずつ減らすと、答えは3ずつ増えます。
この規則を崩さないように、さらに掛ける数を減らすと、
−3×(−1)=3
−3×(−2)=6
−3×(−3)=9
−3×(−4)=12
のように、負の数を掛けることもできます。
このような計算をいろいろやっていくと、次のようなことが分かります。
| (負の数)×(負の数)の答えは、正の数になり、絶対値どうしの掛け算をすればよい。 |
上へ
負の数で割る
6÷3 は、3 に何を掛ければ 6 になるかを求める計算だと考えると、
6÷(−3)=−2
−6÷3=−2
−6÷(−3)=2
などの、負の数の入った割り算をすることができます。
負の数に関する掛け算・割り算について、以下のことがいえます。
正の数と正の数、負の数と負の数の掛け算/割り算を同符号の掛け算/割り算といい、答えは正の数になります。
正の数と負の数、負の数と正の数の掛け算/割り算を異符号の掛け算/割り算といい、答えは負の数になります。
答えの絶対値は、絶対値どうしの掛け算/割り算の答えになります。 |
上へ
負の指数
2×2×2 のように、2を3回掛けた数を 23 と書き「2の3乗」と読みます。
例: 24=2×2×2×2=16
33=3×3×3=27
23 の右肩の3を指数といいます。
3を何乗かしてみます。
34=81
33=27
32=9
このように、指数を1ずつ減らすと、答えは1/3倍になります。
この規則を崩さないように、さらに指数を減らすと、
31=3
30=1
3-1=1/3
3-2=1/9
3-3=1/27
のように、1乗、0乗、負の指数も計算することができます。
一般に、次のような性質があります。
上へ
「算数・数学」の部屋に戻る