問題
a≦x≦a+4を定義域とする関数f(x)=x2−6x+aの最大値を表す関数をG(a)とするとき、G(a)の最小値を求めよ。
解答
f(x)=x2−6x+a=(x−3)2+a−9
より、 y=f(x) のグラフは、(3,a−9) を頂点とする、下に凸のグラフです。
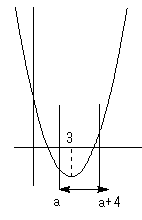
a≦x≦a+4 において、範囲の両端の f(a) か f(a+4) の大きい方が、最大値となりますが、
a=1 を境にして、
(1)a≦1 のとき f(a)=a2−5a が最大値
(2)a≧1のとき f(a+4)=a2+3a−8 が最大値
となります。
これらのグラフを描くと、以下のようになります。
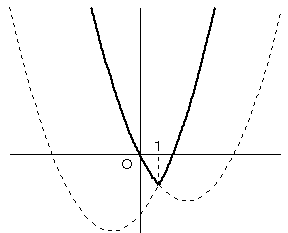
よって、G(a)の最小値は、a=1 のとき、−4
算数・数学の部屋に戻る