問題
平面上に三角形OABがあり、点Pは8s+15t=6を満たす
変数s、tを用いて
OP=sOA+tOB
で表される。
(1)点Pはある定直線上を動く。この直線と直線OA,OB
との交点をそれぞれC,Dとするとき
OC=(ア/イ)OA, OD=(ウ/エ)OB
である。
(2)△PAB=(1/3)△OABのとき
OP=(オ/カ)OA+(キ/クケ)OB
である。
解答
(1)
8s+15t=6
は、
(4/3)s+(5/2)t+1
と書けます。ここで、
u=4s/3,v=5t/2
とおくと、
OP=sOA+tOB=(3u/4)OA+(2v/5)OB=u(3/4)OA+v(2/5)OB
よって、
OC=(3/4)OA
OD=(2/5)OB
とおくと、
OP=uOC+vOD u+v=1
と書けるので、点Pは、直線CD上にあります。
答え ア=3,イ=4,ウ=2,エ=5
(2)
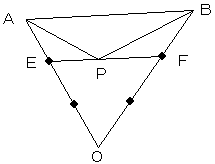
点Pは、上図のように、OA、OBの3等分点で、それぞれ点A、点Bに近い方の点を結んだ直線上にあります。
OE=(2/3)OA
OF=(2/3)OB
とおくと、
OP=sOA+tOB=(3/2)sOE+(3/2)tOF 3s/2+3t/2=1
とおけます。これと、8s+15t=6 を連立させて、s、t を求めると、
s=4/7、t=2/21
答え オ=4,カ=7,キ=2,クケ=21
算数・数学の部屋に戻る