問題
a,bを定数とする。
関数f(x)=x3+ax2+bx は x=1 で極大となり、極小値は0である。
このときのa,b,f(x)の極大値,極小値を取るxの値をそれぞれ求めなさい。
解答
まず、f(x) には、定数項がないので、f(0)=0 であることがわかる。
つまり、y=f(x) のグラフは原点を通る。
さらに極小値が0であることより、y=f(x) のグラフは、以下の2通りが
考えられるが、x=1で極大となることより、左の方のグラフは不可である。
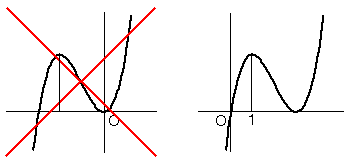
これより f(x) は、
f(x)=x(x−α)2
の形になる。展開して
f(x)=x3−2αx2+α2x
微分して、
f'(x)=3x2−4αx+α2
f'(1)=0 より、
f'(1)=α2−4α+3=(α−1)(α−3)=0
より、 α=1,3
α>1より、α=3
よって、
f(x)=x3−6x2+9x
であるので、
答:a=−6,b=9,x=1で極大、x=3で極小
算数・数学の部屋に戻る