問題
2点A(1,0),B(0,2)があり、f(x)=x2−2ax+b(a,bは定数)とする。y=f(x)が、線分ABと共有点を持つとき、次の各問いに答えよ。
(1) a,bのみたすべき条件をab平面上に図示せよ。
(2) a2+bの最小値を求めよ。
解答
(1)
この問題は、ABを通る直線
y=−2x+2
とy=f(x) を連立させた、
x2−2(a−1)x+(b−2)=0
が、0≦x≦1で少なくとも1つの実解を持つためのa,bの条件を求める問題と考えられます。
g(x)=x2−2(a−1)x+(b−2)
とおきます。y=g(x) のグラフは下図の3通りが考えられます。
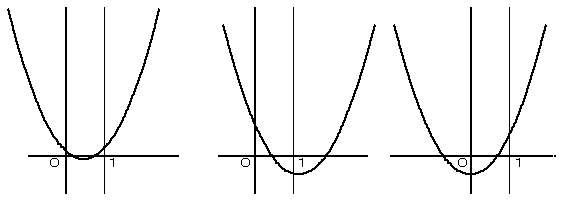
1つは、2解とも 0≦x≦1 にある場合、他の2つは解の一方だけ 0≦x≦1 にある場合です。
2解とも 0≦x≦1 にある条件は
・D≧0
・x=0のとき g(x) の値が0以上。つまり g(0)≧0
・同様に g(1)≧0
・軸が 0≦x≦1 にある
以上より不等式を書くと、
D/4=(a−1)2−b+2≧0 より b≦(a−1)2+2・・・(1)
g(0)=b−2≧0 より b≧2・・・(2)
g(1)=b−2a+1≧0 より b≧2a−1・・・(3)
軸:x=a−1 より 0≦a−1≦1 よって 1≦a≦2・・・(4)
これらの共通部分をグラフに描くと以下のようになります。
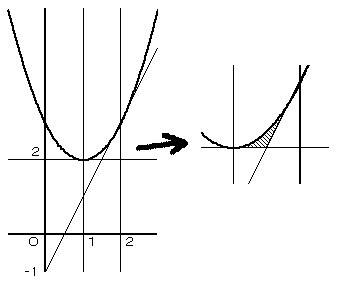
解の一方だけが 0≦x≦1 にある条件は、g(0) と g(1) が異符号であること
(いずれか、または両方が0である場合も含む)よって、
g(0)≦0 かつ g(1)≧0
または
g(0)≧0 かつ g(1)≦0
これをグラフに描くと以下のようになります。
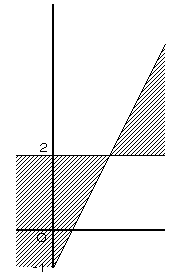
以上2つのグラフを合わせると、以下のようになります。
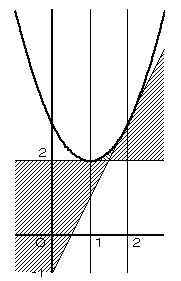
(2) a2+b=k とおきます。
b=−a2+k のグラフは、上に凸のグラフで、kに伴って、b軸に平行に動きます。
このグラフが上のグラフの斜線部と共有点を持ちながら、出来るだけ下に移動した
限界がkの最小値となります。それは、結局 b=2a−1 と接するときです。
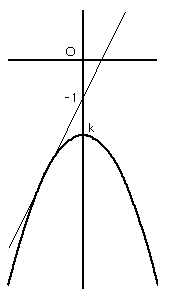
b=−a2+k と b=2a−1 を連立させて、
−a2+k=2a−1
a2+2a−(1+k)=0
D/4=12+(1+k)=2+k=0
よって、k=−2 が a2+b の最小値となります。
算数・数学の部屋に戻る