真優さんからの質問１

問題
(1)放物線x=pt², y=2pt (-1≦t≦1)と直線x=p(p＞0)で囲まれた図形の面積Sを求めよ。また、その図形をx軸の周りに回転してできる回転体の体積を求めよ。
(2)x=t², y=t³ (0≦t≦2)とx軸, 直線x=4で囲まれた図形の面積Sを求めよ。
(3)r=2asinθ (0≦θ≦π)で囲まれた図形の面積を求めよ。(a＞0)
(4)r=a(1+cosθ) (0≦θ≦2π)で囲まれた図形の面積を求めよ。(a＞0)

解答
(1)
　x=pt², y=2pt
より、
pt=y/2 を、px=(pt)² に代入して
　4px=y²
これと、x=p とをグラフに描くと、下のようになります。

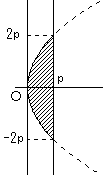
求める面積Ｓは、
　x=y²/4p
を、x=p から引いた部分を ｙ=-2p から y=2p まで積分します。
　

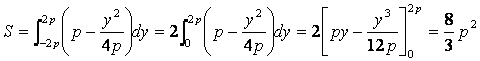
求める体積Ｖは、
　πy²dx＝4pπxdx
を、x=0 から x=p まで積分します。
　

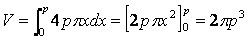
(2)
　0≦ｘ≦4，0≦ｙ≦8 なので、グラフは、下のようになります。

　ｙ＝ｘ^3/2 と書けるので、これをx=0 から　x=4 まで積分します。
　

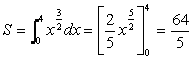
(3)
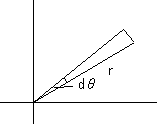
極座標の場合、ｒ と、微小角dθ とで出来る、図のような三角形のような
形の面積は、　dS＝(1/2)ｒ²dθ で表されます。

　r=2asinθ
のとき、dS＝2a²sin²θdθ と書け、これを、θ=0 から θ=π まで積分すると、


(4)
(3) と同様に考えて、
　dS＝(1/2)a²(1+cosθ)²dθ をθ=0 から θ=2π まで積分します。


算数・数学の部屋に戻る