軸が1未満
f(1)>0
D/4=a2−(2a2−5)
=−a2+5≧0
より、-√5≦a≦√5 ・・・(a)
軸の式は x=−a より、
−a<1
よって、 a>−1 ・・・(b)
f(1)=2a2+2a−4>0
より、
2(a−1)(a+2)>0
a<−2 または a>1 ・・・(c)
(a)(b)(c) より
1<a≦√5
=2(a−1)(a+2)<0
より、
−2<a<1
優さんからの質問1
問題
aは実数とする。xの二次方程式x2+2ax+2a2−5=0について、
(1)2つの解がともに1より小さいとき、aの値の範囲を求めよ。
(2)1つの解が1より大きく、他の解が1より小さいとき、aの値の範囲を求めよ。
解答
y=f(x)=x2+2ax+2a2−5 のグラフを考えます。
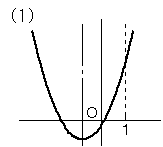
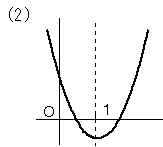
グラフが下に凸であることは明らかなので、各問いの条件を満たすグラフは以下の通りです。
| グラフ |  |
 |
| 満たすべき条件 | 判別式が0以上 軸が1未満 f(1)>0 |
f(1)<0 |
| 解答 | 判別式をDとすると D/4=a2−(2a2−5) =−a2+5≧0 より、-√5≦a≦√5 ・・・(a) 軸の式は x=−a より、 −a<1 よって、 a>−1 ・・・(b) f(1)=2a2+2a−4>0 より、 2(a−1)(a+2)>0 a<−2 または a>1 ・・・(c) (a)(b)(c) より 1<a≦√5 |
f(1)=2a2+2a−4 =2(a−1)(a+2)<0 より、 −2<a<1 |