まりさんからの質問２

問題
次の関数のグラフを、凹凸、変曲点まで調べてかけ。
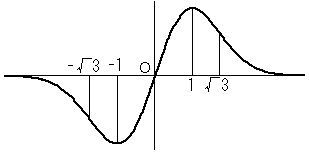
(1) y=xe^-x2/2
(2) y=x²logx
(3) y=2x-1/x²

解答
(1)
　ｙ’＝(x)’(e^-x2/2)＋ｘ(e^-x2/2)’
ここで、
　(e^-x2/2)’＝e^-x2/2×(−ｘ²/2)’＝−ｘe^-x2/2
よって、
　ｙ’＝e^-x2/2−ｘ²e^-x2/2＝(１−ｘ²)e^-x2/2
また、
ｙ”＝−２ｘe^-x2/2−(１−ｘ²)ｘe^-x2/2＝(ｘ³−３ｘ)e^-x2/2
以上より、
ｙ’＝０ となるのは、
　ｘ＝±１
ｙ”＝０ となるのは、
　ｘ＝０，±√3
増減表を書くと

ｘ		-√3		−１		０		１		√3
ｙ’	−	−	−	０	＋	＋	＋	０	−	−	−
ｙ”	−	０	＋	＋	＋	０	−	−	−	０	＋
ｙ		-√3ｅ-3/2		-ｅ-1/2		０		ｅ-1/2		√3ｅ-3/2

(2)
　ｙ’＝2ｘlogｘ＋ｘ＝ｘ(2logｘ＋１)
　ｙ”＝(2logｘ＋１)＋２＝2logｘ＋３
以上より
ｙ’＝０ となるのは
　ｘ＝０，ｅ^-1/2　　（ただし、ｘ＝０ は定義域外）
ｙ”＝０ となるのは
　ｘ＝ｅ^-3/2
増減表を書くと

ｘ	０		ｅ-3/2		ｅ-1/2
ｙ’	×	−	−	−	０	＋
ｙ”	×	−	０	＋	＋	＋
ｙ	×		-3/2ｅ3		-1/2ｅ

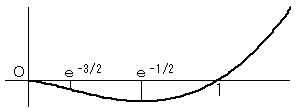
(3)
　ｙ’＝２＋２/ｘ³
　ｙ”＝−６/ｘ⁴
以上より
ｙ’＝０ となるのは
　ｘ＝−１
ｙ” は常に負
増減表を書くと

ｘ		−１		０
ｙ’	＋	０	−	×	＋
ｙ”	−	−	−	×	−
ｙ		−３		×

算数・数学の部屋に戻る