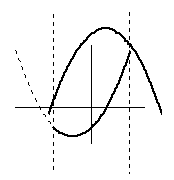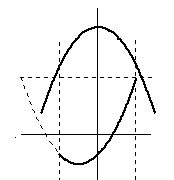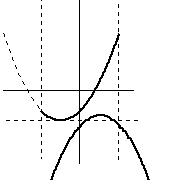まいまいさんからの質問１

問題
-2 ≦ x ≦ 2 の範囲で、関数
　f(x)=x²+2x-2
　g(x)=-x²+2x+a+1
について、次の命題が成立つようなaの値の範囲をそれぞれ解答せよ。
　
(1) すべてのxに対して、f(x) < g(x)
(2) あるxに対して、f(x) < g(x)
(3) すべての組x1、x2,に対して、f(x1) < g(x2)
(4) ある組x1,x2に対して、f(x1) < g(x2)

解答
まず、y=f(x) のグラフがどんなふうになるか描いてみます。

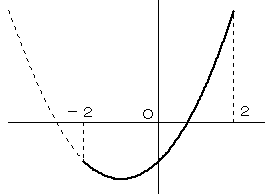
これに y=g(x) のグラフが、そのような位置に来れば、命題を満たすか考えます。
　g(x)＝-x²+2x+a+1＝-(x-1)²+a+2
より、頂点は常に x=1 上にあり、a の値によって、ｙ軸方向に動く。

命題（１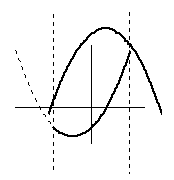）	命題（２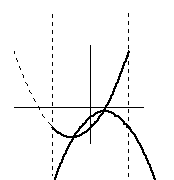）	命題（３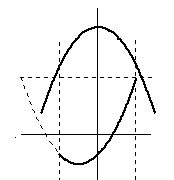）	命題（４）
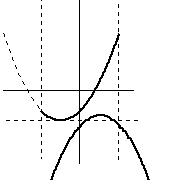範囲全体にわたって、g(x) がf(x) より上にある。	範囲の中でg(x) が f(x) より上にある部分が少しでもある。	範囲全体にわたって、f(x) の最大値よりも g(x) が上にある	範囲の中で、f(x) の最小値よりも g(x) が大きい部分が少しでもある。

以上のような状態です。それぞれ解くと、

命題（１）
　g(-2)＞-f(-2)＝-2 かつ g(2)＞f(2)＝６ より、
　g(-2)＝a-7＞-2 より a＞5
　g(2)＝a+1＞6 より　a＞5　　よって、a＞5

命題（２）
　２つのグラフが接する位置より、ａが少しでも大きければいいので、
　f(x)＝g(x) が重解を持つ場合を考えます。
　（一般の場合はもっと詳しく調べる必要がありますが、この問題の場合、
　頂点のｘ座標が一定なので、これで十分です。）
　　x²+2x-2＝-x²+2x+a+1
　　2x²＝a+3
　a+3=0 のとき重解を持つ。よって、　a＞-3

命題（３）
　この範囲での f(x) の最大値は、６であるので、
　g(-2)＞6 かつ g(2)＞６
　g(-2)＝a-7＞6 より、a＞13
　g(2)＝a+1＞6 より　a＞5　よって、a＞13

命題（４）
　この範囲での f(x) の最小値は -2　であるので、
　y=g(x) の頂点(1, a+2) において、
　　a+2＞-2　よって、a＞-4

算数・数学の部屋に戻る