問題
(1)直線y=x+1に関して、点Pと対称な点をQとする。
点Pが直線y=2x上を動くとき、点Qはある直線上を動く。
この直線を求めなさい。
(2)直線y=2xに関して、
直線2x+3y=6と対称な直線の方程式を求めなさい。
解答
(1)
点Pから点Qへの写し方は、
・y軸方向に−1移動
・y=xに関して対称移動
・y軸方向に1移動
直線y=2x上の点は、(t,2t)と表せます。
上記の手順に沿って写すと、
(t,2t)→(t,2t−1)→(2t−1,t)→(2t−1,t+1)
x=2t−1,y=t+1 とおいて、tを消去すると、
x=2y−3 または y=(x+3)/2
(1)の別解
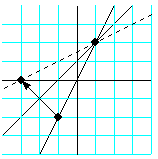
図のように、求める直線は、(1,2)、(-3,0) を通る直線になり、
傾き1/2 なので、
y=(1/2)(x+3)
答え y=(x+3)/2
(2)
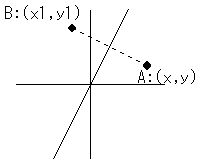
点A(x,y) がy=2xに関する対称移動で、点B(x1,y1)に移ったとすると、
・ABの傾きは-1/2
・ABの中点は y=2x 上にある
の2つの条件が必要。
ABの傾きは (y−y1)/(x−x1)=−1/2
より、 2(y−y1)=x1−x ・・・(1)
ABの中点は((x+x1)/2,(y+y1)/2) であり、これが y=2x 上にあるので、
(y+y1)/2=(x+x1) ・・・(2)
(1)(2)より、
x1=(4y−3x)/5
y1=(3y+4x)/5
以上より、点(x,y)は点((4y−3x)/5,(3y+4x)/5)に写る。
2x+3y=6 上の点は、(3t,2-2t) と表せる。これを
(x,y)→((4y−3x)/5,(3y+4x)/5)
で、変換すると、
((8-17t)/5,(6+6t)/5)
に写る。
x=(8-17t)/5,y=(6+6t)/5
とおいて、tを消去すると、
6x+17y=30
「算数・数学」の部屋に戻る