問題
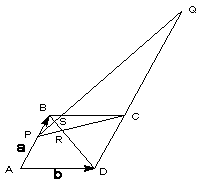
平行四辺形ABCDにおいて、AB=a、AD=bとおく。
辺ABを3:2に内分する点をPとし、辺DCを3:2に外分する点をQをする。
線分PCと線分BDの交点をRをするとき、PRを求めよ。
また線分PQと線分BDの交点をSとするとき、PSを求めよ。
解答
AP=3a/5
AC=a+b
より、
PC=AC−AP=2a/5+b
一方、△BPRと△DCRの相似比より、
PR:RC=BP:CD=2:5
よって、
PR=2PC/7
=4a/35+2b/7
AQ=3a+b
より、
PQ=AQ−AP=12a/5+b
一方、△BPSと△DQSの相似比より、
PS:SQ=BP:DQ=2:15
よって、
PS=2PQ/17
=24a/85+2b/17
「算数・数学」の部屋に戻る