問題
関数f(x)=x3-3a2xの0≦x≦1における最大値、最小値を求めよ。ただし、a>0とする。
解答
f'(x)=3x2-3a2 なので、x=±a で、f'(x)=0 となり、以下のようなグラフになります。
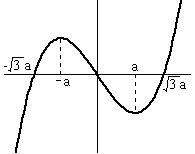
0≦x≦1 での最大、最小の現れ方は、aの値によって、以下のように分類できます。
高2さんからの質問2
問題
関数f(x)=x3-3a2xの0≦x≦1における最大値、最小値を求めよ。ただし、a>0とする。
解答
f'(x)=3x2-3a2 なので、x=±a で、f'(x)=0 となり、以下のようなグラフになります。
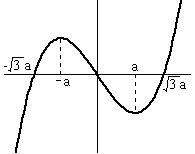
0≦x≦1 での最大、最小の現れ方は、aの値によって、以下のように分類できます。
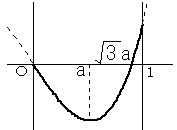 |
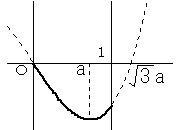 |
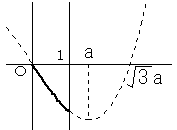 |
| √3a<1 のとき つまり、 0<a<3/√3 のとき f(a) が最小値 -2a3 f(1) が最大値 1−3a2 |
3/√3≦a<1 のとき f(a) が最小値 -2a3 f(0) が最大値 0 |
a≧1 のとき f(1) が最小値 1−3a2 f(0) が最大値 0 |