問題
2つの曲線 y=3x2(x≧0), y=1/3(x-4)2 (x≧0) と x軸で囲まれた図形をDとする。
D内にあり、1辺がx軸上にある長方形の面積の最大値を求めよ。
解答
グラフは以下のようになります。
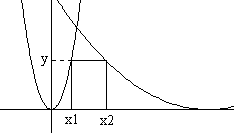
図のようにx1,x2 を決めると、
x1=√(3y)/3
x2=4−√(3y)
と書けます。
長方形の面積Sは
S=(x2-x1)y=(4−4√(3y)/3)y
=4y−(4√3/3)y3/2
z=√y とおいて、0<z<√3 でのSの最大値を求めると、
S(z)=4z2−(4√3/3)z3
S'(z)=8z−4√3z2
S'(z)=0 となるのは、z=0,2√3/3 のとき。増減表は、