問題
n×nの正方形ABCDを,碁盤の目のように,一辺が1の正方形がn2個できるように区切ります.
そのとき対角線ACに交わる長方形の数はいくつになるのでしょうか?
長方形の頂点が対角線ACに触れる場合も交わると見なします.
解答
まず、すべての長方形の数を求めます。
ある格子点を考えて、その点より右かつ下にある点の個数がその格子点を
左上の頂点とする長方形の数です。
4×4の場合とn×nの場合の図を描きます。
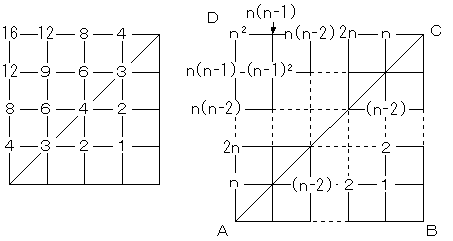
長方形の総数は、格子点上の数をすべて足して、
Σi=1〜n(Σj=1〜n ij)= Σi=1〜nn(n+1)i/2=n2(n+1)2/4
このうち、対角線と離れているものは、対角線ACよりも右下にある格子点に
示された長方形の数の総数になります。
1{1+2+・・・(n-2)}+2{1+2+・・・(n-3)}+・・・+(n-3)(1+2)+(n-2)・1
=Σi=1〜n-2Σj=1〜n-1-iij=Σi=1〜n-2i(n-1-i)(n-i)/2
=Σi=1〜n-2{i3−(2n-1)i2+n(n-1)i}
=(n4−2n3−n2+2n)/24
=(n-2)(n-1)n(n+1)/24
対角線の左上にも同じ数だけあるので、それらを、長方形の総数から引くと、
n2(n+1)2/4−2(n-2)(n-1)n(n+1)/24
=n(n+1)(n2+3n−1)/6 ・・・答え
算数・数学の部屋に戻る