問題
容器Aには5%の食塩水が300g、容器Bには20%の食塩水が200g入っています。
これらに対して、A,Bからそれぞれxgの食塩水を取り出し、AからのものをBに、BからのものをAに入れ、よくかきまぜる。
このとき、A,Bの食塩水の濃度が等しくなるようなxの値を求めなさい。
これを、天秤算を使って解いて下さい。
解答
「天秤算」は食塩水天秤法ともいわれ、その名の通り、食塩水の濃度の問題でよく使われます。
天秤を考え、
さおの方向に濃度の目盛り、各濃度の位置にその濃度の重さに相当するおもりをつるしたと考えた場合、
天秤がつり合う位置の目盛りが、混ぜた後の濃度になります。
上の問題で、5%の食塩水300gと、20%の食塩水200gを混ぜたときの濃度を求めます。
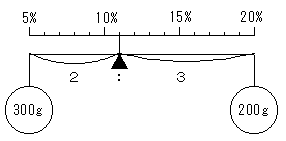
図のように、 腕の長さ×おもりの重さ が等しいとき天秤はつり合いますから、
腕を2:3に内分する点でつり合い、これは目盛りでいうと、11%の位置なので、
混ぜた結果は、11%になります。
確かに、混ぜた後の
食塩の重さ:300×5%+200×20%=15+40=55
食塩水の重さ:300+200=500
なので、濃度は、55÷500=11% になります。
問題の「A,Bの食塩水の濃度が等しく」なっている状態でも、濃度が11%ずつになっているはずです。
よって、AとBの混ぜる割合も同じ 3:2 になっているはずなので、
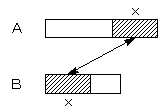
Aの入っていた容器において、
(300−x):x=3:2
より、
3x=2(300−x)
x=120
(Bの入っていた容器において、 x:(200−x)=3:2 としても同様です)
算数・数学の部屋に戻る