数さんからの質問１

問題１
条件　x²+y²=4 のもとで、2x²+y²+2y-2 の最大値、最小値を求めよ。

問題２
y=x+|3x-1| の -1≦x≦2における最大値と最小値を求めよ。

解答１
x²+y²=4 より、 x²=4-y² ただし -2≦y≦2
これを、2x²+y²+2y-2 に代入して、
　2(4-y²)+y²+2y-2=-y²+2y+6
　　=-(y-1)²+7
-2≦y≦2 より、
　y=1 (x=±√3) のとき 最大値 7
　y=-2 (x=0) のとき 最小値 -2

解答２
x＜1/3 のとき y=x-(3x-1)=-2x+1
x≧1/3 のとき y=x+(3x-1)=4x-1
これより、y=x+|3x-1| のグラフは、以下のようになる。

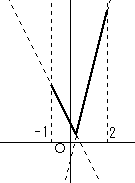
よって、
　x=1/3 のとき、最小値 1/3
　x=2 のとき、最大値 ７

「算数・数学」の部屋に戻る