問題
2つの関数y=x2-4x, y=k(x-a) のグラフが、どんなkの値に対しても
-2≦ x ≦2の範囲で少なくとも1つの共有点をもつようなaの値の範囲を求めよ。
解答
y=k(x-a) は、点(a, 0) を通る、傾きkの直線です。
この問題は、点(a, 0) を通る直線を、点(a, 0)を中心に回転させたとき
(直線がy軸に平行になる場合を除いて)常に、放物線 y=x2-4x の
-2≦ x ≦2 の部分と交わるような、a の値を求めるものです。
原点における接線を、x軸の負の方向に任意の長さ動かすと、放物線より
離れた直線になるので、aを、a<0 の範囲に取ることは出来ません。
よって、a≧0 として考えます。
下図において、放物線の実線が、-2≦ x ≦2 の部分となります。
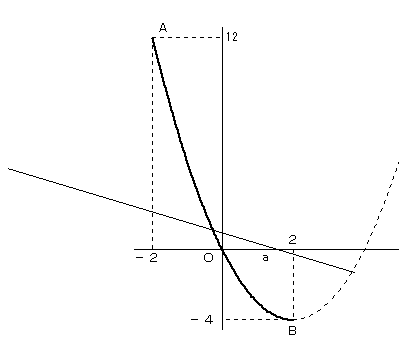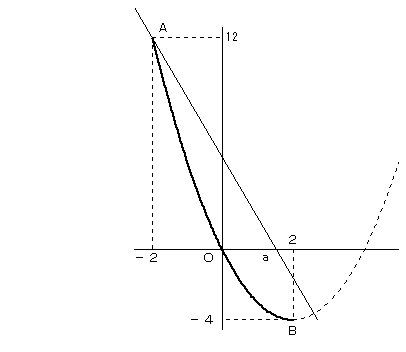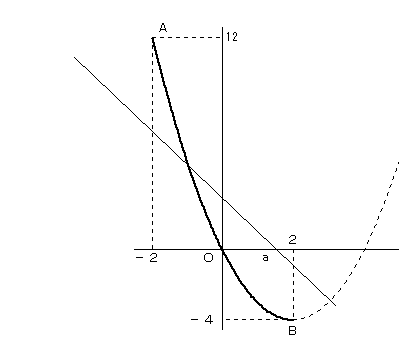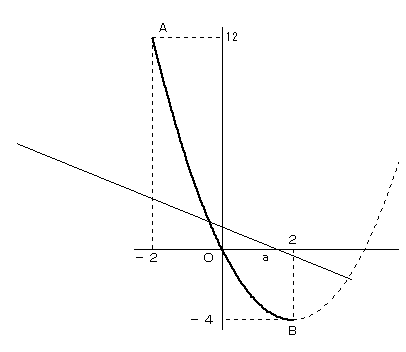
aが図のような位置のとき、直線が点Aを通る位置から、さらに立てる
(kが負で、さらに小さくなる)と、直線は、放物線の実践部分と、交点を持たなくなります。
そうならないようにするためには、
直線が点A に達したときにもう一端が、点Bに達していなければなりません。
点Bについて考えた場合も同様です。
よって、2点A,B を通るときを考えると、
y=−4x+4=−4(x−1)
より、a=1 となります。
aが、この値以下であれば、条件を満たします。
答え 0≦a≦1
算数・数学の部屋に戻る