問題
５以上の自然数ｎについて、座標平面上の第一象限で直線ｘ+ｙ＝ｎより下にあり、x座標、y座標がもとに整数である点を考える。
この中の異なる４点を頂点とし、辺が軸に平行な長方形の個数をａnとする。このとき次の問いに答えよ。
(1)数列 {ａn} が満たす漸化式を求めよ。
(2)数列 {ａn} の一般式を求めよ。・・・・・・ヨッシーが追加
解答
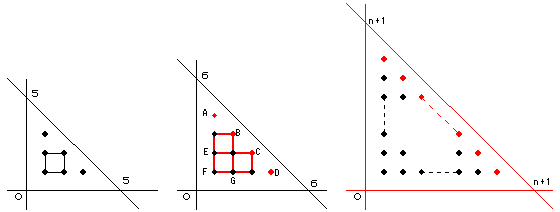
ｎ＝５の時は ａ5＝１ です。
ｎ＝６になったとき、新たに A, B, C, D の４点が増えます（上図の赤い点）。
黒い点だけで出来る長方形は、既にｎ＝５のところで、数えているので、
ｎ＝６になったときに増えた長方形は、赤い点を頂点に持つ長方形です。
A を頂点に持つ長方形はなし。
B を頂点に持つ長方形は、B より左下にあるE, F と B とが対角線になるような長方形で、合わせて２つ。
C を頂点に持つ長方形は、C より左下にあるF, G と C とが対角線になるような長方形で、合わせて２つ。
D を頂点に持つ長方形はなし。
で、合計４個、増えています。
一般に、ｎ が ｎ＋１ になったときに増える点は、（ｎ＋１）−２＝ｎ−１ 個です。
座標でいうと、(1, n-1), (2,n-2), (3, n-3), ……… (n-3, 3), (n-2, 2), (n-1, 1) です。
点(1, n-1) を頂点に持つ長方形はなし。
点(2, n-2) を頂点に持つ長方形は、この点より左下に 1×(n-3) 個の点があるので、n-3 個。
点(3, n-3) を頂点に持つ長方形は、この点より左下に 2×(n-4) 個の点があるので、2(n-4) 個。
・・・・・・
点(k, n-k) を頂点に持つ長方形は、この点より左下に (k-1)×(n-k-1) 個の点があるので、(k-1)(n-k-1) 個。
・・・・・・
点(n-2, 2) を頂点に持つ長方形は、この点より左下に (n-3)×1 個の点があるので、n-3 個。
点(n-1, 1) を頂点に持つ長方形はなし。
長方形がない場合も、それぞれ、0×(n-2)個、(n-2)×0個、と書けるので、
ｎ＋１ になったときに増えた長方形の数(ａn+1−ａn)は、
(k-1)(n-k-1)
を、ｋ＝１から ｎ−１ まで合計した数。
よって、
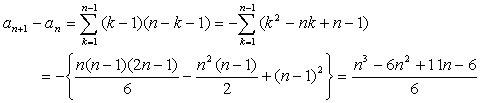・・・・・・(1) の答えｎ≧５ のときの階差数列が、上のような式なので、数列 {ａn} は、ｂn＝(ｎ3−６ｎ2＋１１ｎ−６)/６ を使って、
次のように表される。
ａ5＝１， ａn＝ａ5＋Σk=5〜n-1ｂn＝ａ5＋Σk=1〜n-1ｂn−Σk=1〜4ｂn
よって、
ａn＝(ｎ4−１０ｎ3＋３５ｎ2−５０ｎ＋２４)/２４
なお、
ａn＝(ｎ−１)(ｎ−２)(ｎ−３)(ｎ−４)/２４
となり、
ａ1＝ａ2＝ａ3＝ａ4＝０
となるので、ｎ≧５ に限らず、任意の自然数ｎについて、
ａn＝(ｎ4−１０ｎ3＋３５ｎ2−５０ｎ＋２４)/２４
と書いて良い。
算数・数学の部屋に戻る