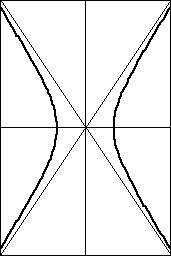
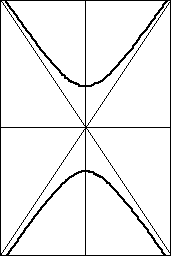
反比例と双曲線
双曲線とは
ある2点からの距離の差が一定の点の集まりを双曲線といいます。
このときの2点を焦点といいます。
双曲線の一般式
双曲線の一般式は以下の通りです。符号によって、2通りの形状があります。
 |
 |
|
| 焦点:(± |
焦点(0,± |
原点を通る2直線 bx±ay=0 を漸近線といい、双曲線のグラフは、
この線に限りなく近づいていく。ただし、交わることはない。
反比例の式
xとyとが反比例するとき、その式は
xy=a (a≠0)
と書けます。
そのグラフは以下の通り。下図は a>0 の場合。
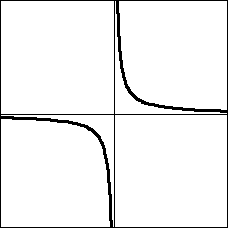 →
→ 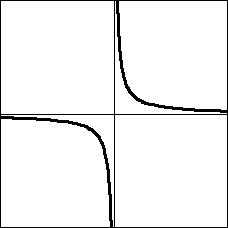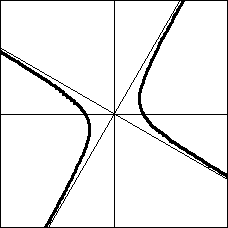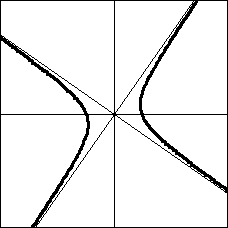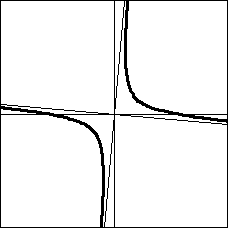
これを−45°回転させます。
x=xcos45°−ysin45°
y=xsin45°+ycos45°
を、xy=a に代入して、
(xcos45°−ysin45°)(xsin45°+ycos45°)=a
(x−y)(x+y)=2a
x2/2a−y2/2a=1
となり、双曲線の式と一致します。
a>0のとき (√(2a),√(2a))、(−√(2a),−√(2a))
a<0のとき (−√(2a),√(2a))、(√(2a),−√(2a))
が焦点となります。
漸近線は x軸(=0) と y軸(x=0) です。