紅さんからの質問４

問題
方程式x³+px+q=0（ただしｐとｑは実数）が、３つのお互いに異なる実数解をもつための必要十分条件を求めよ。

解答
ｙ＝ｆ（ｘ）＝ｘ³＋ｐｘ＋ｑ のグラフは、おおむね次のようになる。

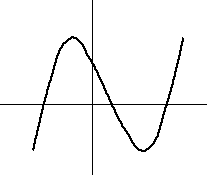
つまり、極大値と極小値が、異符号であれば、条件を満たします。
　ｙ’＝３ｘ²＋ｐ
ｙ’＝０　が、異なる２実解を持つためには
　ｐ＜０
このとき、ｙ’＝０ を解いて、
　ｘ＝±√(-p/3)
条件より、
　ｆ(−√(-p/3))＞０　・・・(1)
　ｆ(√(-p/3))＜０　　・・・(2)

以上より、
　ｐ＜０　かつ　２ｐ√(-p/3)＜３ｑ＜−２ｐ√(-p/3)

算数・数学の部屋に戻る