紅さんからの質問３

問題
　ｆ(x)=x³+kx²+x+1　が　x＞0　の領域で極小値をもつような定数kの値の範囲を求めよ。

解答
　ｙ＝ｆ（ｘ） のグラフは、おおむね次のような形状となります。

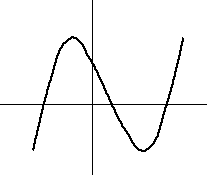
よって、ｆ’（ｘ）＝０ が異なる２実解を持ち、その大きい方の解が、正であれば、
条件を満たします。

　ｆ’（ｘ）＝３ｘ²＋２ｋｘ＋１
判別式：Ｄ/４＝ｋ²−３＞０ は必須。
また、　ｆ’（０）＝１　なので、２解は、ともに負かともに正。
ともに正になるには、軸：ｘ＝−ｋ／３ について、−ｋ／３＞０ であること。

以上より、　ｋ＜−√３

算数・数学の部屋に戻る