三角形の三辺の長さ a,b,c が分かっているとき、三角形の面積Sは、
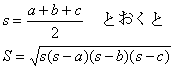
と表せる。
ヘロンの公式(幾何的証明)代数的証明はこちら
三角形の三辺の長さ a,b,c が分かっているとき、三角形の面積Sは、
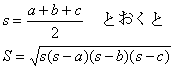
と表せる。
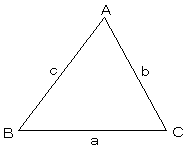 |
以下の説明では、左図のように、頂点および角度をA,B,Cで表し 各頂点に向かい合う辺の長さを、a,b,c で表します。 |
予備知識1(内接円に関する性質)
△ABCの内接円の各接点から頂点までの長さは下図の通り。
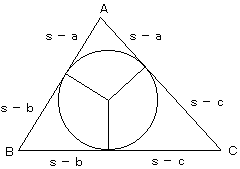
AE=AF, BD=BF, CD=CE
より、
AF+BD+CD=(a+b+c)/2=s
一方、
BD+CD=a
より、
AF=s-a
他も同様。
予備知識2(傍接円に関する性質)
△ABCの辺BCの外側に描いた傍接円において、頂点Aから引いた接線の
長さは s である。他の2つの傍接円についても同様。
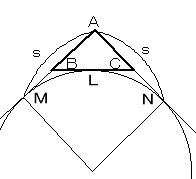
BL=BM, CL=CN
より、
MA+NA = a+b+c = 2s
MA=NA より、
MA = NA = s
証明
図のように、面積を求める△ABCの内接円および傍接円を描きます。
内接円の中心をD、ABとの接点をE、半径をr、
傍接円の中心をF、ABとの接点をG、半径をRとします。
このとき、求める面積Sは
S=rs
です。
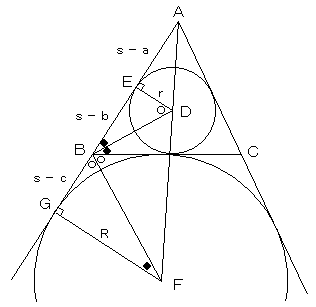
上述の予備知識、および等しいことがわかっている角を図に書き込むと
上図のようになります。
ここで、△ADE、△AFG、△BDE、△FBGを抜き出すと、以下のようになります。
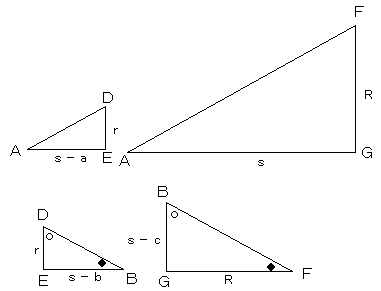
△ADEと△AFGが相似であることより、
rs=R(s−a) ・・・(1)
△BDEと△FBGが相似であることより、
rR=(s−b)(s−c) ・・・(2)
(2) および r>0 より
R=(s−b)(s−c)/r
(1) に代入して、
r2s=(s−a)(s−b)(s−c)
両辺にsを掛けて平方根を取ると、
S=rs=√{s(s−a)(s−b)(s−c)}
となり、ヘロンの公式が導かれる。
「算数・数学の部屋」に戻る