はてなさんからの質問１
問題
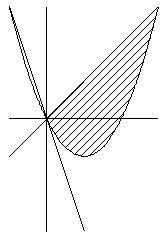
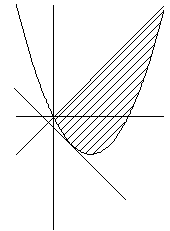
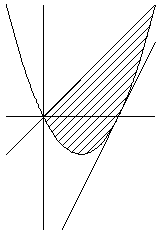
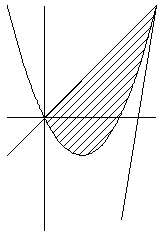
実数ｘ，ｙが不等式 ｘ−ｙ≧０ および ｘ2−２ｘ−ｙ≦０ をみたす時、
ｙ−ａｘの最大値および最小値を求めよ。（ａは定数）
解答
たとえば、ｙ−２ｘ の最大最小を求めよという問題なら、ｙ−２ｘ＝ｋ とおいて、
直線 ｙ＝２ｘ−ｋ が当該範囲と共有点を持ちながらｋが変化するときの
上限下限を求めれば良いです。
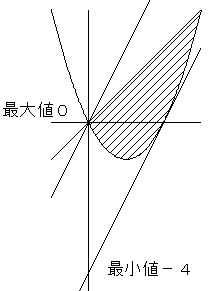
今回の問題は、直線の傾きがいろいろの場合があるので、最大、最小の
現れ方もそれぞれ異なってきます。そこで、以下のように場合分けします。
ただし、ｙ−ａｘ＝ｋ とおきます。直線の式は ｙ＝ａｘ＋ｋ となります。
 |
ａ＜−２のとき (0,0) を通る点で最小値 ０ (3,3) を通る点で最大値 3-3a |
 |
−２≦ａ＜１ のとき 放物線と接するとき最小値-(a+2)2/4 (3,3) を通る点で最大値 3-3a |
 |
１≦ａ＜４ のとき 放物線と接するとき最小値-(a+2)2/4 (0,0) を通る点で最大値 ０ |
 |
４≦ａ のとき (3,3) を通るとき最大値 3-3a (0,0) を通るとき最小値 ０ |