問題
円C:x2+y2+6x-4y+8=0と直線L:x-3y+14=0があり、円Cと直線Lは2点A,Bで交わっている。ただし、Aのx座標はBのx座標より小さい。
(1)2点A,Bの座標を求めよ。
(2)点Aにおける円Cの接線の方程式を求めよ。
(3)x,yが2つの不等式
x2+y2+6x-4y+8≦0 x-3y+14≦0
を満たすとき、-mx+yの最大値は6である。定数mの値を求めよ。
解答
(1)
x2+y2+6x-4y+8=0 と x-3y+14=0 を連立させて、
A:(-5,3)、B::(-2.4)
(2)
円Cの式は
(x+3)2+(y-2)2=5
と書けます。
公式
(x-a)2+(y-b)2=c2
の、円上の(x0,y0) における接線は、
(x-a)(x0-a)+(y-b)(y0-b)=c2
である。
より、点A(-5,3) における接線は
-2(x+3)+(y-2)=5
y=2x+13
(3)
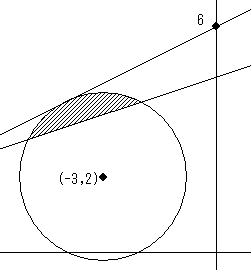
-mx+y=k とおくと、
y=mx+k
より、kはこの直線のy切片になります。
図のように、円Cに接してy切片が6の直線が求める直線です。
円:(x+3)2+(y-2)2=5 上の点(x0,y0) における接線は、
(x+3)(x0+3)+(y-2)(y0-2)=5
これが(0,6) を通ることより
3(x0+3)+4(y0-2)=5 ・・・(i)
また、点(x0,y0) は、円C上の点なので、
(x0+3)2+(y0-2)2=5 ・・・(ii)
(i)(ii) を解いて、(x0,y0)=(-4, 4) または (x0,y0)=(-4/5,, 8/5)
図を満たすのは (x0,y0)=(-4, 4) であり、このときの傾きは
m=(6-4)/(0+4)=1/2
算数・数学の部屋に戻る