問題
平面上の△ABCとその内部の点Pに対して、4PA+5PB+6PC=0 が成り立ち、直線APと辺BCの交点をMとする。
(1)AMをAB、ACを用いて表せ。
(2)点Pが△ABCの内接円の中心であるとき、3辺の長さの比AB:BC:CAを最も簡単な整数比で表せ。
(3)点Pが△ABCの外接円の中心で、外接円の半径が1のとき、内積PA・PBを求めよ。
解答
(1)
4PA+5PB+6PC=0
を変形して
4AP=5PB+6PC=5(AB−AP)+6(AC−AP)
これより、
15AP=5AB+6AC
AP=(5AB+6AC)/15
ここで、点Mは、直線AP上にあるので、AM=kAP と書けます。つまり、
AM=kAP=(5k/15)AB+(6k/15)AC
と書けますが、点Mは、BC上の点なので、AB と AC の係数において、
5k/15+6k/15=1
が成り立ちます。つまり
11k/15=1
より、k=15/11 となり、
AM=(5AB+6AC)/11
と書けます。
(2)
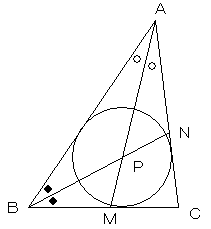
直線BPと辺ACの交点をNとすると、(1) と同様にして、
BN=(4BA+6BC)/10=(2BA+3BC)/5
と書けるので、
AN:NC=3:2
また、(1)より、
BM:MC=6:5
点Pが△ABCの内接円の中心であるので、
AMは、∠BACの二等分線、BNは、∠ABCの二等分線になるので、
角の二等分線の定理より、
AB:AC=BM:MC=6:5
BA:BC=AN:NC=3:2=6:4
よって、
AB:BC:CA=6:4:5
(3)
4PA+5PB+6PC=0
を変形して、
4PA+5PB=6CP
左辺右辺それぞれ、自分自身との内積を取って、
(4PA+5PB)・(4PA+5PB)=36CP・CP
|AP|=|BP|=|CP|=1 に注意して展開すると
16+25+40PA・PB=36
よって、
PA・PB=-1/8
算数・数学の部屋に戻る