問題

解答
(1)
通常通り計算して、
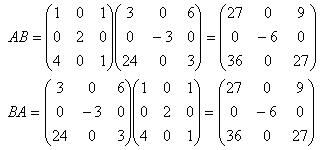
より、AB=BA
としても良いですし、
A=At,B=Bt
および、
AB=(AB)t
であることより、
AB=(AB)t=BtAt=BA
としても良いでしょう。ただし、(AB)t=BtAt を既知のものとしています。
(2)
Aの固有値をλとすると、
Ax=λx
を満たす、0ベクトルでない列ベクトルxが存在します。3次の単位行列をEとすると、
λx=λEx
と書けるので、 Ax=λx は、
Ax=λEx
(A−λE)x=0
と書けます。A−λE の逆行列が存在すると、両辺左からそれを掛けて、
x=0
となり、xが0ベクトルでないことに反するので、A−λE の逆行列は存在せず、
|A−λE|=0
となります。
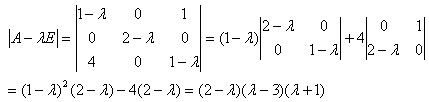
より、Aの固有値は、λ=2,3,-1 となります。
λ=2 のとき、固有ベクトルをx1 とすると、
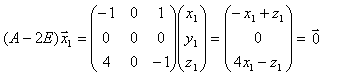
これを解いて、x1=z1=0,y1 は、0以外の任意の実数
よって、固有ベクトルは
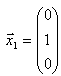
同様にして、λ=3 のとき、固有ベクトルをx2 とすると、
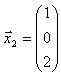
λ=−1 のとき、固有ベクトルをx3とすると、
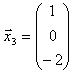
(3)
Bx1=-3x1
Bx2=15x2
Bx3=-9x3
より、x1,x2,x3 は、3つとも、Bの固有ベクトルになっている。
(4)λ=2,3,-1 に対する固有ベクトルを、x1,x2,x3 とすると、
Ax1=2x1
Ax2=3x2
Ax3=−x3
と書け、
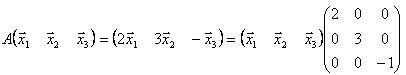
となります。P=(x1 x2 x3 ) とおいて、上の式の左から、P-1を掛けると、
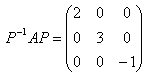
となり、また、
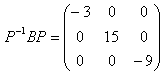
となります。実際にPおよびP-1を計算すると、
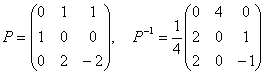
となります。
算数・数学の部屋に戻る