問題
△ABCの内部の点Pが5PA+2PB+3PC=0を満たしているとき,次の比をそれぞれ求めよ。
(1)2点A,Pを通る直線が辺BCと交わる点をDとするときBD:DC
(2)3つの三角形の面積比△ABP:△BCP:△ACP
解答
点A を始点とする 点B,C,P の位置ベクトルをそれぞれ、b, c, p とおく。
5PA+2PB+3PC=0
より、
-5p+2(b-p)+3(c-p)=0
10p=2b+3c
p=(2b+3c)/10=(2b+3c)/5×1/2
(2b+3c)/5 は、BCを 3:2 に内分する点(実はこの点がDになります)の位置ベクトルであり、
点Pはその中点になります(さらに 1/2 を掛けているので)。
つまり、点Pおよび点Dの位置は下図のようになります。
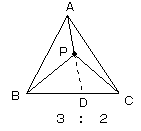
(1)BD:DC=3:2
(2)点PはADの中点なので、
△ABP=△BPD
△ACP=△CPD
また、BD:DC=3:2 より、
△BPD:△CPD=3:2
よって、△ABP:△BCP:△ACP=3:(3+2):2=3:5:2
「算数・数学」の部屋に戻る