1.円の内サイクロイド(トロコイド)
原点中心半径 r1 の円C1の内側を、半径 r2 (r1>r2) の円C2が、接しながら滑ることなく回転するとき、
C2 の中心O2 からの距離が r3 である点Pの描く軌跡。
r3=r2 のときをサイクロイド、それ以外をトロコイドといいます。
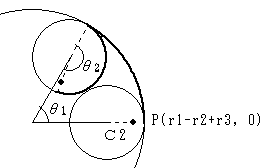
円C2 の中心の位置を((r1-r2)cosθ1, (r1-r2)sinθ1) で表すこととし、θ1=0 のときの点Pの座標を(r1-r2+r3, 0)とします。
円C2 が、円C1 の内側を滑らずに、θ1だけ回転したとき、点Pは、円C2 の中心から見て、θ1−θ2 の方向にあります。
一方、図の円C1上の太線の弧と、円C2上の太線の弧との長さが等しいことより、
r1θ1=r2θ2
よって、
θ2=(r1/r2)θ1
θ1だけ回転したときの、円C2の中心は、
((r1-r2)cosθ1, (r1-r2)sinθ1)
点Pの位置は円C2 の中心から
(r3cos(θ1−θ2), r3sin(θ1−θ2))
だけ進んだ位置にあるので、その座標は、
P:((r1-r2)cosθ1+r3cos(θ1−(r1/r2)θ1), (r1-r2)sinθ1+r3sin(θ1−(r1/r2)θ1))
とくに、サイクロイドの場合、r3=r2 であるので、
P:((r1-r2)cosθ1+r2cos(θ1−(r1/r2)θ1), (r1-r2)sinθ1+r2sin(θ1−(r1/r2)θ1))
「算数・数学」の部屋に戻る