正多面体は、この5つが存在し、それ以外はあり得ません。
例えば、正三角形だけで出来ている正多面体を考えます。
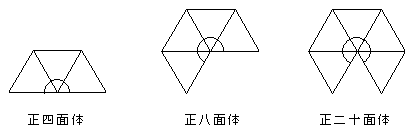
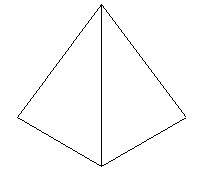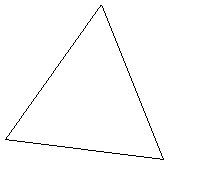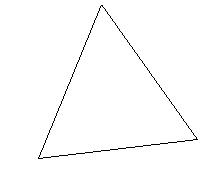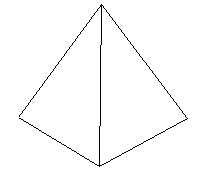
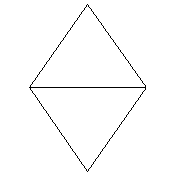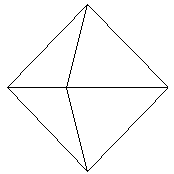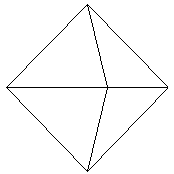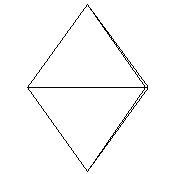
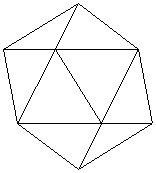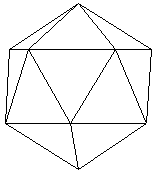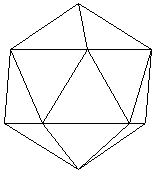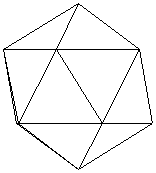
上の図は、各多面体の展開図の一部です。
正四面体は、1つの頂点に正三角形の角が3つ集まっています。
正八面体は4つ、正二十面体は5つです。
さらに、正三角形を1つ増やすと、正六角形ができてしまい、立体に折ることができません。
(へこんだ部分を作ればおれますが、少なくとも正多面体にはなりません)
また、1つの頂点に集まる正三角形が2つしかなかったら?
これは、自分で想像するか、実際に展開図を描いて試してみてください。