問題
内のりが深さ6cm、底面の半径が8cmの円柱形の容器に水がいっぱいに入っている。
この中に、底面の半径が4cmの鉄の円錐を入れて底に安定させたところ、
水が全量の 7/48 だけあふれ出たという。円錐の高さを求めよ。
解答
まず、この容器の容積は、
64π×6=384π (cm3)
であり、その 7/48 は、
384π× 7/48 =56π (cm3)
になります。
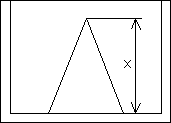
図のような状況を想定すると、円錐の体積は、
16πx/3
となり、
16πx/3=56π
を解くと、
x=10.5
となり、水面から出てしまいます。
そこで、
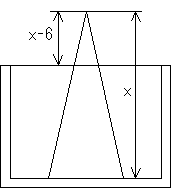
図のような状況であることがわかります。
円錐の体積は 16πx/3 であり、
水面より出ている部分の体積は、円錐全体と相似であり、相似比は、x−6:x。
体積はその3乗に比例するので、水面より出ている部分の体積は、
16πx/3 ×(x−6)3/x3
すると、水の中にある部分の体積は、
16πx/3 − 16πx/3 ×(x−6)3/x3 = 16πx/3 ×{1−(x−6)3/x3}
これが、56πに等しいので、
16πx/3 ×{1−(x−6)3/x3}=56π
両辺 3x2/8π を掛けて
2{x3−(x−6)3}=21x2
展開して整理すると、
15x2−216x+432=0
5x2ー72x+144=0
(x−12)(5x−12)=0
x≧6 の範囲でこれを解くと、
x=12
答え 12cm
「算数・数学」の部屋に戻る