y=x-[x] のグラフは以下の通りです。
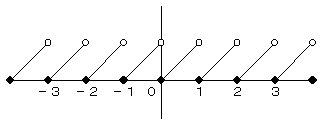
●はその点を含む、○はその点を含まないことを表します。
メタンさんからの質問
問題1
aを実数とする。xの方程式
(x-[x])2=a(x+1)
について次の問いに答えよ。
(1)この方程式が異なる2個の実数解を持つようなaの値の範囲を求めよ。
(2)この方程式が n個(nは1以上)の実数解を持つような
a の値の範囲を求めよ。
解答1
まず、f(x)=x-[x] がどのような関数であるかを調べます。
[x] は一般にはガウス記号と呼ばれ「x を超えない最大の整数」という意味です。
[4.3]=4, [3]=3, [-2.3]=-3 です。
x-[x] は平たく言えば、「x の小数部分」です。具体的に
x-[x] の値を調べてみます。
| x | 0.0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | 1.4 | 1.6 | 1.8 | 2.0 | 2.2 | 2.4 | 2.6 | 2.8 | 3.0 |
| [x] | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 3 |
| x-[x] | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 0 |
このように、[0,1) の範囲の繰り返しになっています。
y=x-[x] のグラフは以下の通りです。

●はその点を含む、○はその点を含まないことを表します。
[0,1) では、y=x で、以下、それの繰り返しです。
同様に、y=(x-[x])2 のグラフは、以下の通りで、やはり [0,1) の繰り返しになっています。
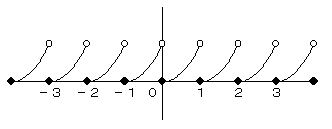
このグラフと y=a(x+1) の交点を調べればいいわけですが、
y=a(x+1) は 点(-1,0) を必ず通ります。
点(-1,0) から、色々な傾きの直線を引いて、y=(x-[x])2のグラフと
2点で交わる範囲を調べると、以下のようになります。
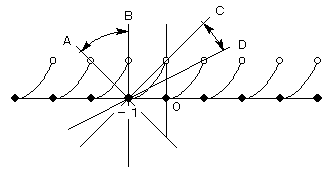
傾き a が直線Aの位置(a=-1) よりも、すこしでも大きいと、3点で交わってしまいますから
a≦−1
一方、小さい方はいくらでもOKです。
直線Bの位置は、傾きで表しようがありませんが、この位置では1点でしか交わらないので
問題なしです。
また、直線Cの位置(a=1)では交点は1つで、これよりすこしでも傾きが小さければ、交点は2つ以上になります。
一方、直線Dの位置(a=1/2)では交点は2つで、これよりすこしでも傾きが小さければ交点は3つ以上になります。
以上より、
1/2≦a<1
答え(1) a≦−1 または 1/2≦a<1
同様に考えて、3点で交わる場合は、以下の通り。
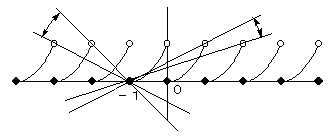
つまり、 −1<a≦-1/2 または 1/3≦a<1/2 である。
一般にn≧3のとき n個の点で交わるためには、
-1/(n-2)<a≦1/(n-1) または 1/n≦a<1/(n-1)
n=2のとき
a≦−1 または 1/2≦a<1
n=1のとき
a≧1
問題2
aはa>1を満たす定数とする。関数
f(x)=ax/(1+ax)
について実数 t が
f(f(t))=f(t)・・・(1)
を満たすとき
f(t)=t
をも満たすことを示せ。
解答2−1
まず、f(x) の逆関数が存在することを示します。
y=ax/(1+ax)
とおき、x について解くと、
x=y/a(1-y) ※a(1-y) が分母
より、
f-1(x)=x/a(1-x)
(1) の両辺について f-1で変換すると、
f-1(f(f(t)))=f-1(f(t))
逆関数の性質:f(f-1(x))=x, f-1(f(x))=x
合成関数の性質(結合法則):f(g(h(x)))=(f・g)(h(x))
より、
f(t)=t
が導ける。
解答2−2
<逆関数の存在を確認するところまでは同じ>
仮に s≠t である s について、
f(t)=s
であると仮定する。
両辺を f-1 で変換すると、
f-1(f(t))=f-1(s)
よって、
t=f-1(s)
一方、(1) より、
f(s)=s
両辺を f-1 で変換すると、
f-1(f(s))=f-1(s)
s=f-1(s)
よって、
t=s=f-1(s)
となり、s≠t に矛盾する。
よって、f(t)=t である。
「算数・数学」の部屋に戻る