問題
同一直線上に無い平面上の三点O,A,BがありOA=5/2,OB=3である。
a=OA,b=OBと表す時、内積 a・b=9/2である。
さらに点Aを中心とする半径3/2の円と点Bを中心とする半径2の二つの交点を
C,Dとし、線分ABと線分CDの交点をEとする。
(1) 線分ABの長さを求めよ。
(2) 線分AEの長さを求めよ。
(3) a,bを用いてOEを表せ。
解答
∠AOB=θとすると、
a・b=OA・OBcosθ=(5/2)・3cosθ=9/2
より、
cosθ=3/5
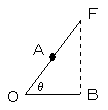
(1)解き方その1
上図のようにOB=3,BF=4、OF=5の直角三角形を考えると、AはOFの中点となります。
AO=AB=AFより、 AB=5/2
解き方その2
余弦定理より、
AB2=OA2+OB2−2OA・OBcosθ=25/4+9−2・(5/2)・3・(3/5)
=25/4
よって、AB>0 より、AB=5/2
(2)
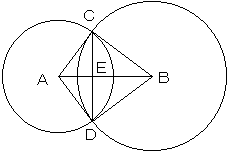
解き方その1
上図において、△ABCは3:4:5の直角三角形です。
いきなり、AE:EB=AC2:BC2=9:16 としてもいいですが、
この公式を知らない人は、以下のようにします。
△BCE、△ACEもそれぞれ、3:4:5の直角三角形なので、
AE:EC=3:4=9:12
EC:EB=3:4=12:16
よって、AE:EB=9:16
AB=5/2 より、
AE=5/2×9/25=9/10
解き方その2
簡単のため、AB=5、AC=3、BC=4とします。
Aを原点、Bを(5,0)として、2つの円の式を作ると、
x2+y2=9 ・・・(1)
(x−5)2+y2=16・・・(2)
(2)から(1)を引いて、
-10x+25=7
x=1.8
実際は、この半分なので、AE=1.8÷2=0.9