問題
三角形の3つの頂点から、それぞれの対辺またはその延長上に下ろした垂線は、1点で交わる。
この交点を、その三角形の垂心という。
3点A(a,4)、B(0,0)、C(5,0)を頂点とする三角形がある。
この三角形の重心をG、垂心をHとする。
(1)GとHの座標を求めよ。
(2)△GBCと△HBCの面積の比が16:9のとき、aの値を求めよ。
解答
(1)
Gの座標は、3点A,B,Cの座標の平均なので、
G:((a+5)/3,4/3)
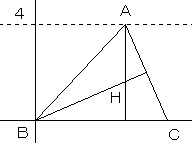
Hのx座標は必ずaであるので、Hの座標を(a,b)とおきます。
a=0 のときは、Hは(0,0)となります。
a=5 のときは、Hは(5,0)となります。
a≠0 かつ a≠5 のとき、
BHの傾きは b/a
ACの傾きは 4/(a−5)
BH⊥ACより、これらの積が−1となり、
(b/a)4/(a−5)=−1
これをbについて解いて、
b=(5−a)a/4
以上より、Hの座標は H:(a,(5−a)a/4)
(2)
(1) の結果より、
△GBC:△HBC=4/3 : (5−a)a/4 =16:9
または
△GBC:△HBC=4/3 : (5−a)a/4 =16:−9
これを解いて、
「算数・数学」の部屋に戻る