問題
平行四辺形ABCDにおいて、
辺ADを2:1に内分する点をEとし、
線分BEを1:3に内分する点をFとする。
また、三角形ABCの重心をGとする。
直線ABと直線FGの交点をHとするとき、
比AH:HBおよびHF:FGを求めよ。
解答
(以下、太字はベクトルを表します)
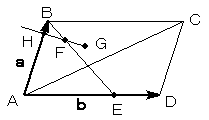
a=AB、b=AD とおきます。
すると、
AC=a+b
と書けます。また、
AE=2b/3
AF=(3AB+AE)/4
より、
AF=(9a+2b)/12
と書け、
AG=(AA+AB+AC)/3
より、
AG=(2a+b)/3
と書けます。
直線GH上の任意の点をPとすると、実数tに対して、
AP=(1−t)AF+tAG
と書けるので、これをa、bで表すと、
AP=(9−t)a/12+(1+t)b/6
となります。点Pが点Hの位置にあるとき、
AP=sa (sは実数)
の形に書けるので、bの係数は0になります。よって、
t=−1
このとき、
AH=10a/12=5a/6
よって、 AH:HB=5:1 とわかります。
また、
HF=AF−AH=(−a+2b)/12
HG=AG−AH=(−a+2b)/6
これより、
HG=2HF
となり、 HF:FG=1:1 となります。
「算数・数学」の部屋に戻る