問題
(1)2次不等式x2+(a-1)x-2a2-2a ≦ 0 を満たすxの範囲を求めよ。
(2)(1)で求めた x の範囲における2次関数 y=x2+axの最小値が 0 であるように a の値を定めなさい。
解答
(1)
左辺を因数分解して、
{x-(a+1)}(x+2a)≦0
a+1<-2a のとき、つまり、a<-1/3 のとき、 a+1≦x≦-2a
a+1≧-2a のとき、つまり、a≧-1/3 のとき、 -2a≦x≦a+1
(2)
(i) a<-1/3 のとき
y=x2+ax のグラフは、以下の通りです。
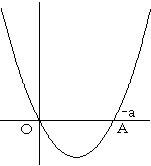
ある範囲の最小値が0になるためにはその範囲の
右端が点Oである または 左端が点Aである
場合です。
よって、
-2a=0 より a=0 ・・・ a<-1/3 に反するので不適
a+1=-a より a=-1/2 ・・・ OK!
(ii) -1/3≦a<0 のとき
y=x2+ax のグラフは、(i) と同様です。
右端が点Oである または 左端が点Aである
点も、同様です。よって、
a+1=0 より a=-1 ・・・ 不適
-2a=-a より a=0 ・・・ この際不適(本当はOKですが、a=0 については別途調べます)
(iii) a=0 のとき
(1) の不等式は
x2-x ≦ 0
となり、この解は、 0≦x≦1。
この範囲における y=x2+ax=x2 の最小値は x=0 のとき y=0 であるので、条件を満たす。
a=0
(iv) a>0 のとき
y=x2+ax のグラフは、以下の通りです。
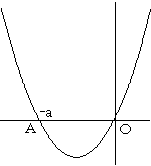
(i) と同様に、
右端が点Aである または 左端が点Oである
場合を考えます。
a+1=-a より、a=-1/2 ・・・ 不適
-2a=0 ・・・不適
以上より、 a=0 または a=-1/2
算数・数学の部屋に戻る