と表される。このとき、地図によると、
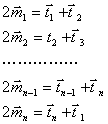
が成り立つ。ところが、木の位置
言いかえられる。
問題9の解答
島の適当な地点を原点Oにとると、
![]()
と表される。このとき、地図によると、
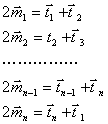
が成り立つ。ところが、木の位置 ![]() はわからなくなってしまっているから、問題は次のように
はわからなくなってしまっているから、問題は次のように
言いかえられる。
が与えられているとき、(1) を満たすベクトル
が存在するという
仮定のもとで、が定まるだろうか?
(i) n=2p(偶数)のとき、(1) より
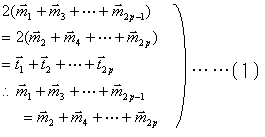
したがって、(1) を満たす ![]() が存在するという仮定の下で
が存在するという仮定の下で ![]() を与えれば
を与えれば
![]() は
は
![]()
によって、一意的に確定する。
(ii) n=2p+1(奇数)のとき
![]() が決まれば
が決まれば ![]() も確定し、逆に
も確定し、逆に ![]() が決まると
が決まると![]()
も確定する。実際、![]() が与えられたとすると、(1) の第1式から第n−1式より
が与えられたとすると、(1) の第1式から第n−1式より
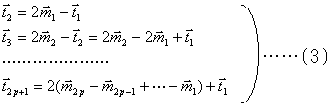
また、(1) の第n式より
![]()
したがって、(3) の最後の式より
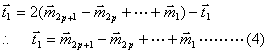
これからまた(3)により、順に ![]() が
が ![]() によって表されることになる。
によって表されることになる。
特に、(4) より
![]()
であり、![]() は
は ![]() のみでなく
のみでなく ![]() も与えないと決定できないことがわかる。
も与えないと決定できないことがわかる。
以上より、太郎君は宝を、nが偶数のときは (2) によって見つけることができるが、
nが奇数のときは見つけることができない。………(答)
解答を寄せて下さった皆さん。ありがとうございました。
| 数楽者 さん |
| hisoka さん |
| 中村明海 さん |