問題８の解答

問題にも書いたとおり、この問題は、もともと空間図形の問題だったのを、平面に置き換えたのですが、
元の問題が、手元にないので、当時の模範解答がわかりません。
わかり次第載せますが、とりあえず、２通りの解法を載せておきます。

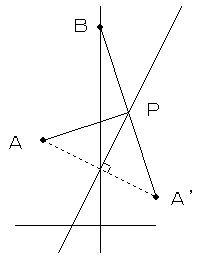
（解法１）対称点を使う方法					直線ｍに関して、点Ａと対称な点をＡ’とすると、 ｍ上の任意の点Ｐについて、ＡＰ＝Ａ’Ｐとなるため Ａ’Ｐ＋ＢＰが最小の時、ＡＰ＋ＢＰも最小になります。 直線ｍの傾きは２なので、直線ＡＡ’の傾きは 　−１÷２＝−１／２ です。よって、直線ＡＡ’の式は、 　ｙ−３＝-1/2（ｘ＋２） 　ｙ＝−ｘ／２＋２ これと、直線ｍ　ｙ＝２ｘ＋２　との交点は（０，２） で、これは、線分ＡＡ’の中点である。 よって、Ａ’の座標は、 　（０×２＋２、２×２−３）＝（２，１） Ａ’Ｂを通る直線の傾きは、（７−１）／（０−２）＝−３ よって、直線Ａ’Ｂの式は、 　ｙ＝−３ｘ＋７ これと、直線ｍとの交点が求める点Ｐであり、その座標は、 （１，４）　　　　　　　　答え　（１，４）
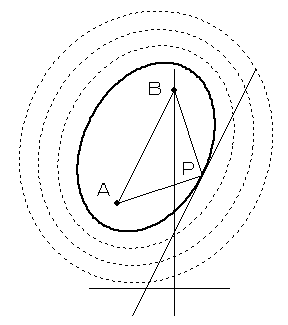
（解法２）ＡＢと直線ｍが平行であることを 　　　　　利用する方法					(YokoyaMac さんの回答) まず，直線ＡＢの傾きが２であることから， 　直線AB//直線m ということが分かる。さらに，直線ｍのｙ切片である（０，２）は 点Ａから直線ｍへ下ろした垂線の足であるから，これを点Ｃとする。 この時，点Ｂから直線ｍへ下ろした垂線の足は，（２，６）であり、 これを点Ｄとする。 さて，ＡＰ＋ＢＰを一定にして点Ｐを動かすと，２点Ａ，Ｂを焦点とする 楕円が描ける。 すなわち，ＡＰ＋ＢＰを最小にしたいなら，Ａ，Ｂを焦点とするできるだ け小さい楕円を，直線ｍと共有点を持つように描き，その共有点の座標を 求めればよいことになる。 この場合，直線ｍと接するような楕円を描けばよい。 そうすると求める点Ｐは，直線ｍとその楕円との接点ということになり， 直線ＡＢと直線ｍが平行であることを考えれば，ＡＢの中点から直線ｍ へ下ろした垂線，すなわち，２点Ｃ，Ｄの中点を求めればよい。 よって，点Ｐの座標は，（１，４） 　　　　　　　　　　　　　　　答え　（１，４）

解答を寄せて下さった皆さん。ありがとうございました。

問題に戻る

「算数・数学の部屋」に戻る