1:α
とします。
近似値を使うと
α=0.8
であり、三角関数を使うと
α=cos36°
です。

問題15の解答
| 図1のように、1つの角が36°である直角三角形の斜辺と、36°をはさむもう1つの | |
| 辺の長さの比を 1:α とします。 近似値を使うと α=0.8 であり、三角関数を使うと α=cos36° です。 |
 |
<外側の正20面体と正12面体の関係>
| 図2において、A,B,C,D,EおよびOは正20面体の頂点であり、辺OB,OEの中点をF,G、線分AF,AGをそれぞれ2:1に内分する点をM,Nとします。(点M,点Nは△OAB、△OAEの重心です) このとき、 BE=AB×2α であり、中点連結定理より FG=BE÷2 より、 FG=AB×α また、 より、 正12面体の1辺の長さは、外側の正20面体の1辺の2α/3倍である。・・・・(1) |
 |
<正12面体と内側の正20面体の関係>
| 図3において、5角形ABCDEは正12面体の1つの面、太線は正12面体の5つの面の重心を結んだ正5角形で、その辺は内側の正20面体の辺になっています。 今、CD:FGを求めようとするとき、 図3(立体の平面図)において、 △CDOと△FGOは相似 なので、 CD:FG=OC:OF となります。 図4は5角形ABCDEの平面図です。 この図より OH:OF=1+α:1+2α であることがわかります。 図3において、 OH=OC×α 以上より、 内側の正20面体の1辺の長さは、正12面体の |
  |
(1)(2)より、
内側の正20面体の1辺の長さは、外側の正20面体の辺の![]() 倍です。
倍です。
![]()
を代入して計算すると
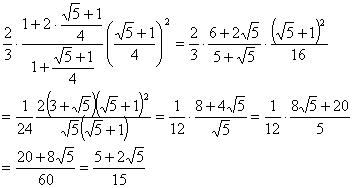
より、
外側の正20面体:内側の正20面体=15:![]() ・・・・(答え)
・・・・(答え)
また、近似値α=0.8を使うと、 675:416 になります。
※近似値を使用した場合は、計算方法により、多少の違いが出る可能性があります。
解答を寄せて下さった皆さん。ありがとうございました。
| europa さん |
| 貞松 篤 さん |
| Hamayan さん |