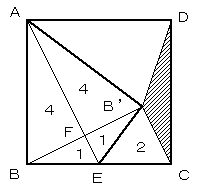
△B'ECの面積を2とすると、
BE=CEゆえ △B'BE=△B'EC=2 △BEFと△B'EFは合同であるから
△BEF=△B'EF=1
次に二つの直角三角形 △ABFと△BEFは相似で相似比はAB:BE=2:1なので △ABF=4
また△ABFと△AB'Fは合同なので、△AB'F=4
△ABEは正方形ABCDの4分の1の面積なので
全体の面積は20
△ABB'+△B'CDは正方形の面積の半分なので、
△ABB'+△B'CD=10
ゆえに△B'CD=2
答え △B'CDは正方形の1/10倍の面積である
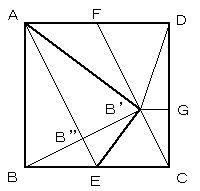
B' からCDに下ろした垂線の足をGとするとき
CB':CF=B'G:FD・・・・・・(1)
ところでEA//CFなので、FD=AD/2・・・・・・(2)
BB'とAEの交点をB''とすればEB'':B''A=1:4・・・・・・(3)
(3)からCB':EA=2:5・・・・・・(4)
(2),(4)から B'G:FD=2:5
よって B'G:AD=1:5
よって 面積比は1:10
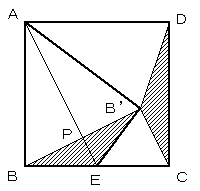
すると、BとB'はAEを軸にした線対称な図形ですからBB'とAEは垂直に交わります。
よって△EPBや△BPAなどは△ABEと相似になります。
さて、ここで△ABB'と△CDB'の面積の和は正方形全体の半分です。
また△ABB'とEBB'の面積の和も正方形全体の半分の面積です。
ですからCDB'とEBB'の面積は等しいことになります。
前述の相似関係よりEP:PB=1:2 PB:PA=2:4とわかるのでPEはAEの1/5の長さです。
よって三角形EBB'の面積は四角形ABEB'の1/5となって、全体の1/10です。
答;1/10倍
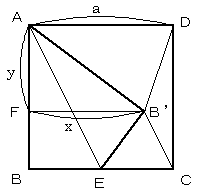
B'から辺ABへの垂線の足をFとする。
B'F=x,AF=yとする。
四角形ABEB'の面積はa2/2。
これを、△AFB’と台形FB’EBに分けて考えると、
xy/2+(a/2+x)(a-y)/2=a2/2
整理すると、
y=2x-a......... .1)
△AFB'は直角三角形で、AB=AB'。
ピタゴラスの定理より、
x2+y2=a2............2)
1),2)より
x=4a/5, y=3a/5
△B'CDの面積は、
a*1/5*a*1/2=a2/10
正方形の面積は、 a*a=a2
したがって、1/10倍となる。
答え 1/10倍
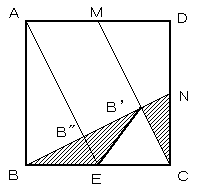
△EB"B,△EB"B',△NB'Cは合同で、 短辺:長辺=1:2の直角三角形である。
つまり、BB":B"B':BN = 2:2:1
よって、△NB'C = 1/5△NBC = 1/20×正方形ABCD
求めるDB'Cはその2倍で、正方形ABCDの 1/10 となる。
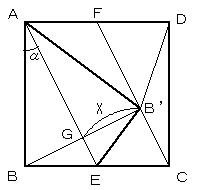
△AB'E∽△AGB'∽△B'GE
∵∠BAE=αとすると
∠AEB=90°−αで、∠ABG=∠AB'G=90°−α
また、∠GBE=∠GB'E=αで、∠BEG=∠B'EG=90°−α
より、AG:GB'=B'G:GE=2:1
B'G=Xとすると、AG=2X、GE=X/2
よって AE=AG+GE=5X/2
□ABCDの面積=Sとすると、
△AEB'の面積=1/2・AE・B'G=X/2・5X/2=5X2/4=S/4
よって、S=5X2
△GB'Eの面積=1/2・GE・B'G=1/2・X/2・X=X2/4
また、△B'BEの面積=△B'ECの面積(∵EはBCの中点) かつ、
△B'BEの面積=2・△GB'Eの面積=2・X2/4=X2/2
よって、△B'ECの面積=X2/2
ここで、△B'ECの面積+△B'FDの面積=S/4=5X2/4 であることがわかり、
△B'FDの面積=5X2/4−△B'ECの面積=3X2/4
よって、△B'ADの面積=2・△B'FDの面積=3X2/2
従って、
△B'CDの面積=S−△B'ADの面積−△B'ECの面積−△ABEの面積−△AB'Eの面積 =S−3X2/2−X2/2−S/4−S/4
=S/2−4X2/2
=5X2/2−4X2/2
=X2/2
=S/10
以上より、△B'CDの面積は正方形ABCDの1/10となります。
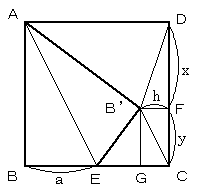
B'より辺CDに垂線をひきその交点をFとし、B'F=h、DF=x、FC=yとする。
辺AB=2aとすると、正方形ABCDの面積は4a2、
△ABEと△AEB'の面積 の和は2a2。
台形AB'FDと台形EB'FCの面積の和は (2a+h)x/2+(a+h)y/2=2a2 ・・・(1)
ここでx+y=2aよりy=2a-x
これを(1)に代入し整理すると
x=2(a-h)、y=2h
B'より辺ECに垂線をひきその交点をGとすると、
B'G=y=2h なので
△B'EGから a2=4h2+(a-h)2
これより h=2a/5
△B'CDの面積は ah なので ah/4a2=h/4a=1/10・・・答え
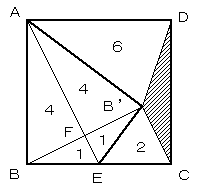
△ABE、△AFB、△BFEは相似だから、
AF:BF=BF:EF=2:1
したがって、
AF:FE=4:1
∴△AFB:△BFE=4:1
△BFEの面積を1とすると、
△B’BE=△B’EC であるから、△B’BCは4
△ABEは5だから、正方形ABCDは20
△AB’D+△B’BCは10になるので、△AB’Dは6
正方形の面積から、△B’CD以外を全て除くと、残りは2
よって、△B’CDは正方形ABCDの 1/10 倍
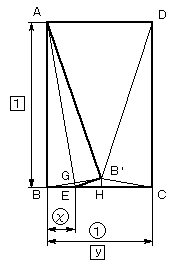
AEとBB’との交点をG、B’からBCへの垂線の足をHとする。
△BB’H と △BEG の相似から
BH:BB’=BG:BE
BB’=2・BG
より
BH=2・BG2/BE…(1)
また、 △ABG と △AEB の相似から
BG:AB=BE:AE
より
BG=AB・BE/AE…(2)
(2) を (1) に代入して、両辺をABで割ると
BH/AB=2・AB・BE/AE2…(3)
また、△ABEにおいて、ピタゴラスの定理より
AE2=AB2+BE2…(4)
(4) を (3) に代入して
BH/AB=2・AB・BE/(AB2+BE2)=2・(BE/AB)/(1+(BE/AB)2)
両辺に AB/BC をかけて整理すると
BH/BC=2・(BE/BC)/(1+(BE/BC)2(BC/AB)2)
BE/BC=x、 BC/AB=y とおくと
BH/BC=2x/(1+x2y2)
であり
△B’CD/□ABCD=HC/2BC=(1−BH/BC)/2=(1−2x/(1+x2y2))/2
この問題では、□ABCD は正方形なので y=1、点EはBCの中点なので x=1/2 とおくと、
△B’CD/□ABCD=1/10
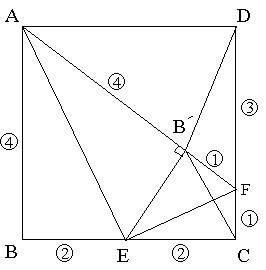
与えられた条件より、
四角形ABEB´と四角形ECFB´は相似で相似比は2:1であることがわかり、
図の○で表す長さの比の関係がわかる。
よって、 □ABCD=1とすると、
CF:FD=1:3 、AB´:B´F=4:1より、
△B´FD=1×3/4×1/2×1/5=3/40
さらに、
FD:CD=3:4より、
△B´CD=△B´FD×4/3=4/40=1/10
したがって、1/10倍である。