問題のコーナー

　あれは、昭和５９年の１月頃。ヨッシーは、西宮にある某Ｈ学園で、Ｍ講師について講師見習いをしていた。教科は算数。今日しも、「弱点補強講座」が終わり、何人かの生徒が、Ｍ講師の周りに集まり、質問をしていた。その中で、ある問題が出された。Ｍ講師は、しばし取り組んでいたが、どうにもうまく解けないようだ。ヨッシーも、しばしの考慮時間の末、ふと解き方がひらめいた時、Ｍ講師から声が掛かった。「ヨッシー君、どうだろう？」。まだ、完全に答えを出すに至っていなかったヨッシーは、おそるおそる黒板に向かった。少しずつ書いているうちに、解けるの解けないのって、どっちだと思う！？って、そう、解けたのであった。生徒たちが言った。「おぉ、出藍の誉れや」。憎たらしいガキやで、ホンマに。

というわけで、当時の問題を掲載しておきます。
ヒマな方は解いてみて下さい。

問題１
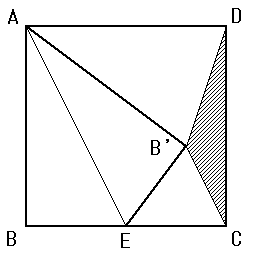
正方形ＡＢＣＤの辺ＢＣの中点をＥとする。
△ＡＥＢをＡＥで折り返したときの頂点Ｂの位置を、Ｂ’とする。
このとき、△Ｂ’ＣＤの面積は、正方形ＡＢＣＤの面積の何倍になるか？

解答受付は終了しました。

「算数・数学の部屋」に戻る