問題
△ABCにおいて、AB=(3,√3),AC=(s,-√3)とする。ただし、s は正の数である。
△ABCの三辺の長さの和が最小となるとき
(1)sはいくらか?
(2)AB・BC+BC・CA+CA・ABはいくらか?
(3)△ABCの外接円の円の中心をRとすると、cos∠BARはいくらか?
※太字はベクトル
解答
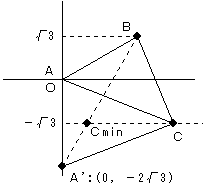
(1)
点Aを原点として、座標上に点B、Cを取ると上図のようになる。
点Cはx軸に平行な直線 y=−√3 上にある。
いま、ABの長さは一定なので、AC+BCが最小となる点Cの位置を見つければよい。
直線y=−√3に対して、点Aと対称な点A’を取ると、AC=A’Cなので、
A’CBが最小になる位置、つまりA’CBが一直線になる位置(上図のCmin)で、ACBも最小となる。
このとき、A’C:A’B=1:3なので、Cの座標は、(1,−√3) 答え s=1
(2)
このとき、AB=(3,√3), CA=(-1, √3)、BC=AC−AB=(-2, -2√3) となる。
AB・BC=3・(-2)+√3・(-2√3)=-6-6=-12
BC・CA=-2・(-1)-2√3・√3=2-6=-4
CA・AB=-1・3+√3・√3=0
よって、 AB・BC+BC・CA+CA・AB=-16
(3)
CA・AB=0 より、∠CAB=90°
よって、△ABCは直角三角形であり、外接円の中心は斜辺BCの中点(2, 0)である。
Rはx軸上にあるので、∠BARはABの角度そのものであり、
∠BAR=30°
よって、
cos∠BAR=√3/2
算数・数学の部屋に戻る