アムロさんからの質問１

問題
(1)原点Ｏを中心とし、半径ｒ、ｒ'の２円がある。
　半径ｒ上の円周上に点Ｐを、半径ｒ'上の円周上に点Ｑをとり、Ｐ(x1，y1)、Ｑ(x2，y2)とすれば
　x1x2＋y1y2＝ｒｒ'cosθ
であることを証明せよ。ただし、θ＝∠ＰＯＱ　とする。
(2)ａとｂのなす角が60度で、|a+b|が|a-b|の２倍になることがあるか否かを調べよ。ただし、|a|＞|b|とする。
　※太字はベクトルです

解答
(1)

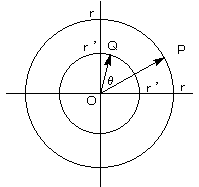
△ＯＰＱにおいて、余弦定理より
　ＱＰ²＝ＯＰ²＋ＯＱ²−２ＯＰ・ＯＱcosθ
　２ＯＰ・ＯＱcosθ＝ＯＰ²＋ＯＱ²−ＱＰ²
　(左辺)＝2rr'cosθ
　(右辺)＝(x1²＋y1²)＋(x2²+y2²)−{(x1-x2)²＋(y1-y2)²}
　　　　＝2x1x2＋2y1y2
　よって、x1x2＋y1y2＝ｒｒ'cosθが成り立つ。

(2)
　|a+b|=2|a-b| であるとする。両辺２乗して
　　|a+b|²=4|a-b|²
　　|a|²＋2a・b＋|b|²=4(|a|²−2a・b＋|b|²)
　　3|a|²-10a・b＋3|b|²＝０
　a・b＝|a||b|cos60°＝|a||b|/2　より
　　3|a|²-5|a||b|＋3|b|²＝０
　|a| についての２次方程式と考えて、判別式Ｄを取ると、
　　Ｄ＝(5|b|)2−4・3・3|b|²＝−11|b|²≦０
　|b|＝０ のとき、|ａ|＝０ となり不適。
　そのほかの場合は、Ｄ＜０ となり、|ａ|は実数解を持たない。
　よって、条件を満たすようなベクトルは存在しない。

算数・数学の部屋に戻る