問題
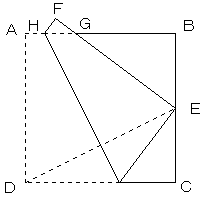
図は、1辺が16cmの正方形ABCDを、頂点Dが辺BCの中点Eに重なるように折った図です。
左上にできる小さな三角形FGHの面積をもとめなさい。
解答
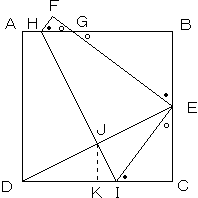
折り目の線をHI(IはCD上の点)とします。
DEとHIの交点Jは、DEの中点です。
点JからCDにおろした垂線の足をKとすると、KはCDの中点となります。
△DEC、△DJK、△JIKは直角をはさむ2辺が 2:1 の相似な三角形であるので
DK=8
JK=DK÷2=4
KI=JK÷2=2
となり、
CI=CK−KI=8−2=6
一方、CE=8 なので、△CEI は3辺の比が、3:4:5 の直角三角形となります。
また、△BGE、△FGH は△CEI に相似な三角形です。
△BGEにおいて、
BE=8
に対して
EG=8×5/3=40/3
よって、FG=16−40/3=8/3
△FGHにおいて、
FG=8/3
に対して
FH=8/3 × 3/4=2
よって、△FGHの面積は
FG×FH÷2=8/3
算数・数学の部屋に戻る