問題
２直線
K： ｘsinα−ycosα＝0
L： ｘsinβ−ycosβ＝0
に関する対称移動をそれぞれ、ｋ、ｌとするとき
合成変換 ｌ・ｋは、2(βーα)の回転であることを示せ。
解答
Ｋ：y=(tanα)x
Ｌ：y=(tanβ)x
であるので、Ｋ、Ｌ はそれぞれ、原点を通り、ｘ軸との角度が、α、βの直線である。
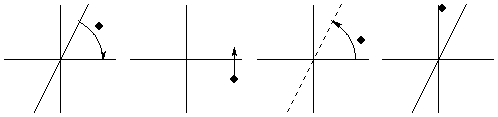
ｘ軸との角度がθの直線に関する対称移動は、図のように、
・−θの回転
・ｘ軸に関して対称
・θの回転
の合成によって、得られる。それを表す行列は、
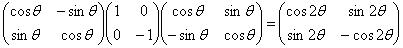（途中の式は省略）よって、ｌ・ｋ を表す行列は、
よって、ｌ・ｋ は2(βーα)の回転となる。
「算数・数学」の部屋に戻る