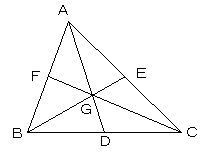
AB//DE かつ AB:DE=2:1
よって、△AGBと△DEGは相似で、相似比は2:1。
よって、BEは、ADを2:1に内分する点Gで交わる。
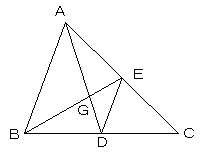
同様に、CFも、ADを2:1に内分する点Gで交わる。
以上より、3直線AD,BE,CFは、一点Gで交わる。
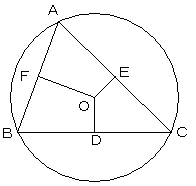
考える。
△OBCにおいて、ODはBCの垂直二等分線なので、
OB=OC
△OCAにおいても同様に、 OC=OA
よって、△OABは、 OA=OB の二等辺三角形なので
AB の垂直二等分線は点Oを通る。
以上より、3辺の垂直二等分線は、一点Oで交わる。
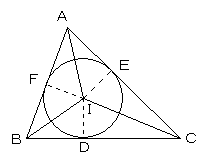
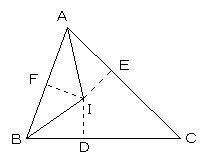
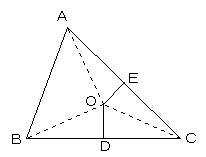
点I からBC,CA,AB におろした垂線の足をD,E,Fとする。
△AEIと△AFI において、
∠AEI=∠AFI=90°
斜辺は共通
∠IAE=∠IAF
よって、△AEIと△AFI は合同となり、IE=IF。
同様に、IF=ID。
よって、IE=ID。
△ICDと△ICE において、
∠IEC=∠IDC=90°
斜辺は共通
ID=IE
よって、△ICDと△ICE は合同となり、∠ICD=∠ICE。
よって、CI は、∠ACBの二等分線となる。
以上より、3つの角の二等分線は、一点Iで交わる。
(辺BCに対して、点Aと反対側に取る)の2等分線は一点で交わる。
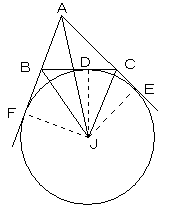
交点Jを考える。
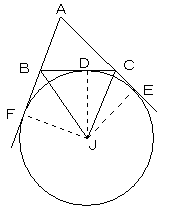
点Jから、BC,CA,ABにおろした垂線の足を、D,E,Fとする。
内心の時と同様に、JF=JD および、JD=JE より、
JF=JE
となり、△JAFと△JAEにおいて、
∠AFJ=∠AEJ=90°
斜辺は共通
JF=JE
より、△JAFと△JAEは合同であり、AJは∠BACの
二等分線となる。
以上より、∠Aの二等分線と、∠B、∠Cの外角の二等分線は一点Jで交わる。
垂線は一点で交わる。
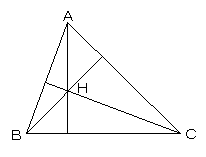
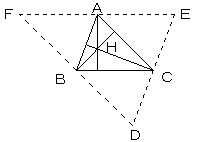
図のように、各頂点を通り、対辺と平行な直線で作られる
三角形DEFを作ると、各垂線は、△DEFの各辺の垂直二等分線となる。
すなわち、△DEFの外心を考えることになり、これは1点に決まるので、△ABCの垂心も1点に決まる。