三次方程式 ｘ3＋ａｘ2＋ｂｘ＋ｃ＝０ の一般解を求めます。
基礎知識１
三次方程式 ｘ3＝１ の解を求めてみます。
ｘ＝１ が解の１つであることは明らかなので、ｘ3−１＝０ の左辺を ｘ−１ をくくり出して因数分解すると
(ｘ−１)(ｘ2＋ｘ＋１)＝０
よって、他の２解は ｘ2＋ｘ＋１＝０ の解となります。実際に解いてみると、
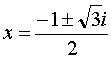（ｉ は虚数単位）となります。このうちのひとつを
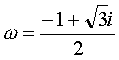とおくと、もう一方は
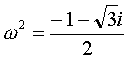となります。この ω、ω2 を、１の原始３乗根といいます。（１の原始ｎ乗根とは、ｎ乗して初めて１になる数です）
ω に関して次の式が成り立ちます。
ω3＝１
ω2＋ω＋１＝０
基礎知識２
ｘ＝ｕ＋ｖ
ｘ＝ωｕ＋ω2ｖ
ｘ＝ω2ｕ＋ωｖ
を解にもつ三次方程式を考えます。条件より
{ｘ−(ｕ＋ｖ)}{ｘ−(ωｕ＋ω2ｖ)}{ｘ−(ω2ｕ＋ωｖ)}＝０
展開して
ｘ3−{(ｕ＋ｖ)}＋(ωｕ＋ω2ｖ)＋(ω2ｕ＋ωｖ)}ｘ2
＋{(ωｕ＋ω2ｖ)(ω2ｕ＋ωｖ)＋(ω2ｕ＋ωｖ)(ｕ＋ｖ)＋(ｕ＋ｖ)(ωｕ＋ω2ｖ)}ｘ−(ｕ＋ｖ)(ωｕ＋ω2ｖ)(ω2ｕ＋ωｖ)＝０
ｘ3−{(ω2＋ω＋１)ｕ＋(ω2＋ω＋１)ｖ}ｘ2
＋{(ω2＋ω＋１)ｕ2＋(ω2＋ω＋１)ｖ2＋３(ω2＋ω)ｕｖ}ｘ−{ｕ3＋(ω2＋ω＋１)ｕ2ｖ＋(ω2＋ω＋１)ｕｖ2＋ｖ3}＝０
ｘ3−３ｕｖｘ−(ｕ3＋ｖ3)＝０
つまり、ｘ2 の項がない三次方程式 ｘ3＋ｂｘ＋ｃ＝０ の解は、
ｂ＝−３ｕｖ、 ｃ＝−(ｕ3＋ｖ3)
となる、ｕ、ｖ に対して、上のように書けます。
準備１
三次方程式 ｘ3＋ａｘ2＋ｂｘ＋ｃ＝０ において、ｘ＝ｙ−ａ/３ とおくと、
(ｙ−ａ/３)3＋ａ(ｙ−ａ/３)2＋ｂ(ｙ−ａ/３)＋ｃ＝０
(ｙ3−ａｙ2＋ａ2ｙ/３−ａ3/２７)＋ａ(ｙ2−２ａｙ/３＋ａ2/９)＋ｂ(ｙ−ａ/３)＋ｃ＝０
ｙ3＋(−ａ2/３＋ｂ)ｙ＋(２ａ3/２７−ａｂ/３＋ｃ)＝０
これで、ｘ2 の項がない三次方程式が出来ました。
解きます
ｍ＝−ａ2/３＋ｂ、ｎ＝２ａ3/２７−ａｂ/３＋ｃ
とおくと、上式は
ｙ3＋ｍｙ＋ｎ＝０
と書けます。
ｍ＝−３ｕｖ、 ｎ＝−(ｕ3＋ｖ3)
となる、ｕ、ｖ を見つけることを目指します。
ｕ3ｖ3＝−ｍ3/２７、ｕ3＋ｖ3＝−ｎ
より、ｕ3、ｖ3 は、二次方程式
ｘ2＋ｎｘ−ｍ3/２７＝０
の２解となります。その一方をα(実数とは限らない)とすると、ｕはαの三乗根の１つ、
ｖは、ｖ＝−ｍ/３ｕ となります。
よって、これら ｕ、ｖ に対して、
ｘ＝ｕ＋ｖ−ａ/３、ωｕ＋ω2ｖ−ａ/３、ω2ｕ＋ωｖ−ａ/３
が、三次方程式 ｘ3＋ａｘ2＋ｂｘ＋ｃ＝０ の解となります。
実際の問題を解きましょう
答えが明らかな三次方程式、例えば、
(ｘ−１)(ｘ−２)(ｘ−３)＝ｘ3−６x2＋１１ｘ−６＝０
を、この方法で解いてみます。途中で、いかにも因数分解できそうなときも
公式の通りに進めます。
ｘ＝ｙ＋２
とおくと、
(ｙ＋２)3−６(ｙ＋２)2＋１１(ｙ＋２)−６＝０
整理して、
(ｙ3＋６ｙ2＋１２ｙ＋８)−６(ｙ2＋４ｙ＋４)＋１１ｙ＋２２−６＝０
ｙ3−ｙ＝０
ここで、上記において、ｍ＝−１、ｎ＝０なので、ｕ3、ｖ3 は、二次方程式
ｘ2＋１／２７＝０
の解となります。これを解いて
ｘ＝±√３ｉ/９
√３ｉ/９ の三乗根の一つは、
ｕ＝(３＋√３ｉ)/６
ｖ＝−ｍ/３ｕ＝２/(３＋√３ｉ)＝(３−√３ｉ)/６
これらに対して、
ｕ＋ｖ＝１
ωｕ＋ω2ｖ＝(−１＋√３ｉ)/２×(３＋√３ｉ)/６＋(−１−√３ｉ)/２×(３−√３ｉ)/６＝−１
ω2ｕ＋ωｖ＝(−１−√３ｉ)/２×(３＋√３ｉ)/６＋(−１＋√３ｉ)/２×(３−√３ｉ)/６＝０
それぞれ ２ を足して、
ｘ＝１，２，３ を得ます。
これは、非常に簡単な例であり、普通は、最終的な解が整数であっても、
複雑な計算になります。
「算数・数学」の部屋に戻る