円 x2+y2=r2 に、円外の点P(a, b) から引いた2本の接線と円との接点をA,B とするとき、
ABを結ぶ直線の式は
ax+by=r2
で表される。
証明
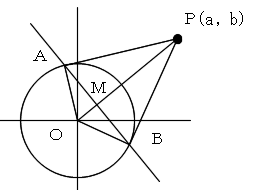
直線ABはOPと垂直なので、
ax+by=c ・・・(1)
の形で表されます。
また、ABとOPの交点をMとすると、
△OAP ∝ △OMA
より、
OM:OA=OA:OP
これより
OM=r2/OP=r2/√(a2+b2)
直線 (1) と原点との距離は
|c|/√(a2+b2)
であり、これがOMにあたるので、
|c|/√(a2+b2)=r2/√(a2+b2)
よって
c=±r2
b>0 のとき
(1) のy切片c/b>0 より c>0
b<0 のとき
(1) のy切片c/b<0 より c>0
b=0 のとき
a>r>0 のとき
(1) の式は x=c/a>0 より c>0
a<−r<0 のとき
(1) の式は x=c/a<0 より c>0
よって、いずれの場合も、直線ABの式は
ax+by=r2
で表されます。
算数・数学の部屋に戻る