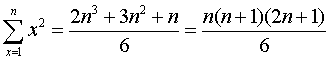
を、図形的に証明します。
自然数の2乗和
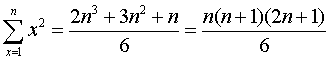
を、図形的に証明します。
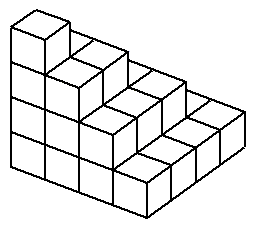
上の図のように、1辺が1の立方体を、12個, 22個, 32個, 42個 ・・・と積んでいき、n段までの個数(体積)
を計算します。
この立体を、下の図のように
・この立体を内包するn×n×nの立方体の3頂点を通る平面
・その平面に平行で、辺1つ分ずらした平面
で、切ります。
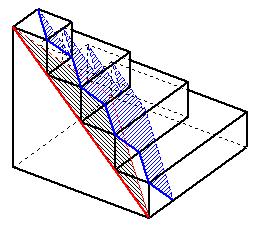
この切断により、各段の立体がどのように分けられるかを見ます。
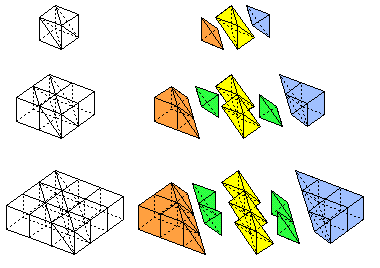
オレンジ色の部分は、すべての段を集めると、
n×n×nの立方体から切り出した、三角錐になります。
その体積は、n3/6
青い部分は、オレンジ色の部分と同じものなので、体積はn3/6
黄色の部分は、1×1×1の立方体から、三角錐を2つ取り除いた立体(体積2/3)
で、上からn段目にはn個存在する。
緑の部分は、1×1×1の立方体から切り出される三角錐(体積
1/6)で、
上からn段目には2(n−1)個存在する。
以上より、この立体の体積は、
n3/6+n3/6+2/3 × n(n+1)/2 +1/6 × n(n-1)=(2n3+3n2+n)/6=n(n+1)(2n+1)/6
立方体から切り出した三角錐とは、
立方体の1つの頂点と隣り合う3つの頂点を通る平面で、
立方体を切るときに出来る、3つの直角二等辺三角形と、
1つの正三角形から出来る三角錐で、体積は、立方体の
1/6 となる。
「算数・数学」の部屋に戻る