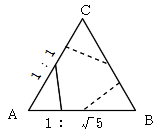正２０面体の座標


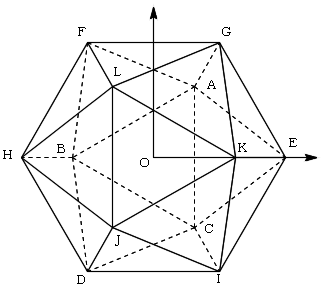
Ａ：(1, √3, (-3-√5)/2)
Ｂ：(-2, 0, (-3-√5)/2)
Ｃ：(1, -√3, (-3-√5)/2)
Ｄ：(-(1+√5)/2, -(1+√5)√3/2, (1-√5)/2)
Ｅ：(1+√5, 0, (1-√5)/2)
Ｆ：(-(1+√5)/2, (1+√5)√3/2, (1-√5)/2)
Ｇ：((1+√5)/2, (1+√5)√3/2, (√5-1)/2)
Ｈ：(-1-√5, 0, (√5-1)/2)
Ｉ：((1+√5)/2, -(1+√5)√3/2, (√5-1)/2)
Ｊ：(-1, -√3, (3+√5)/2)
Ｋ：(2, 0, (3+√5)/2)
Ｌ：(-1, √3, (3+√5)/2)

△ＡＢＣ、△ＥＫＩ、△ＦＧＬ、△ＤＨＪ の重心Ｍ，Ｎ，Ｐ，Ｑを結ぶと正四面体になります。

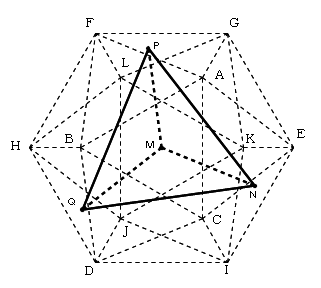
このとき
Ｍ：(0, 0, (-3-√5)/2)
Ｎ：((7+3√5)/6, -√3(1+√5)/6, (3+√5)/6)
Ｐ：(-1/3, (2√3+√15)/3, (3+√5)/6)
Ｑ：(-(5+3√5)/6, -√3(3+√5)/6, (3+√5)/6)

ＮＰのｘｙ平面に平行な平面上での傾きは　-√15/3 であるので、
ＡＣとＮＰのなす角をθとすると、
　tan(π−θ)＝√15/3、tanθ＝3/√15、sinθ＝√(3/8)、cosθ＝√(5/8)
一方、ＡＢとＮＰのなす角をφとすると、φ＝2π/3−θ より
　sinφ＝(√3/2)cosθ＋(1/2)sinθ＝√3(1+√5)/4√2
よって、ＡＢ，ＢＣ，ＣＡを
　sinθ：sinφ＝2：(1+√5)
に内分する点を結んで出来る正三角形は正四面体ＭＮＰＱを原点Ｏを中心に拡大した
四面体を△ＡＢＣで切った断面となります。

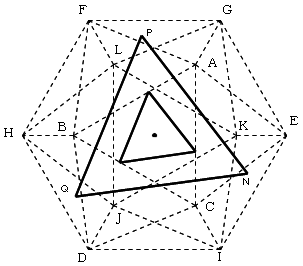
同様に、△ＥＫＩ、△ＦＧＬ、△ＤＨＪ 上にも同じ正三角形を描いて、
線で結ぶと、20面体と辺上で交差する正四面体が出来ます。

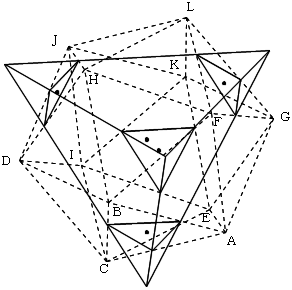
このとき、ＡＢを２；(１+√5) に内分した点Ｒ：((√5-3)/(3+√5), √3(1+√5)/(3+√5), -(3+√5)/2) と、
ＦＧを２；(１+√5) に内分した点Ｓ：(-2/(3+√5), √3(1+√5)/2, (√5-3)/(3+√5)) を結んだ直線が
ｚ軸と交わる点は、
　(0, 0, (3√5-15)/2)
であるので、正四面体ＭＮＰＱ を
　(15-3√5)/(3+√5)＝15-6√5 倍に拡大すると上図の正四面体になります。

さらに、ＡＦの中点Ｔ：((1-√5)/4, √3(3+√5)/4, (-1-√5)/2) から、
　ＲＳ＝(2-√5, √3, 2√5-2)
方向に伸ばした直線が、ｚ軸と交わる点は(0, 0, -(3+3√5)/2) なので
正四面体ＭＮＰＱを
　(3+3√5)/(3+√5)＝3(√5-1)/2 倍に拡大すると、正二十面体と、辺の中点どうしで交わる
正四面体が出来ます。

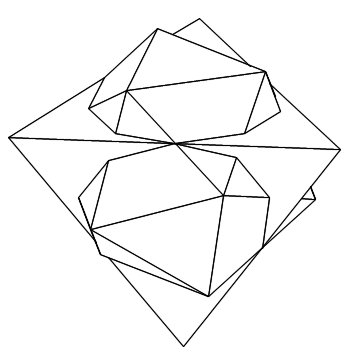
このとき、Ｎ，Ｐ，Ｑのｚ座標は
　(3+√5)/6×3(√5-1)/2＝(1+√5)/2
となります。
辺ＫＥ上でｚ座標が (1+√5)/2 になる点は、ＫＥの中点であるので、
△ＡＢＣ、△ＥＫＩ、△ＦＧＬ、△ＤＨＪ 上の交線は図のようになります。(図は、△ＡＢＣの場合)


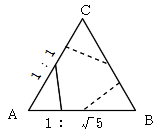
さらに、Ｎ，Ｐ，Ｑ のｚ座標 (3+√5)/6 に対して、Ｊ，Ｋ，Ｌ のｚ座標 (3+√5)/2 は
３倍であるので、正四面体ＭＮＰＱを３倍に拡大すると、正二十面体に外接する
正四面体となります。

これらをつなげて、以下のようなアニメーションを作りました。


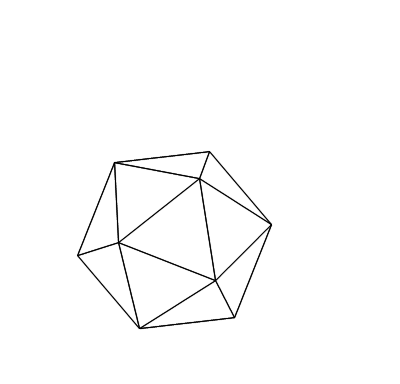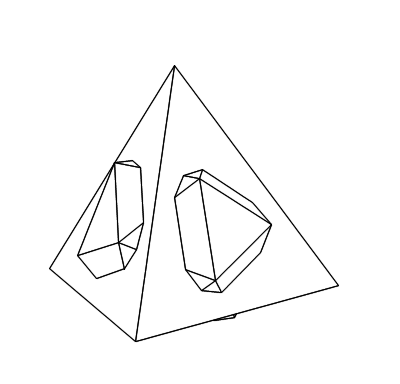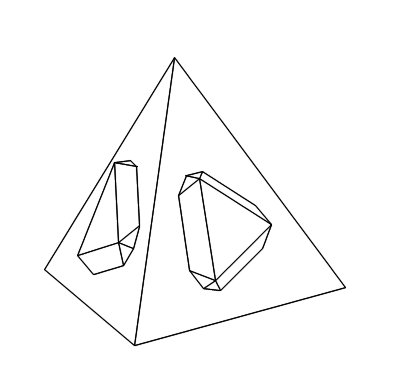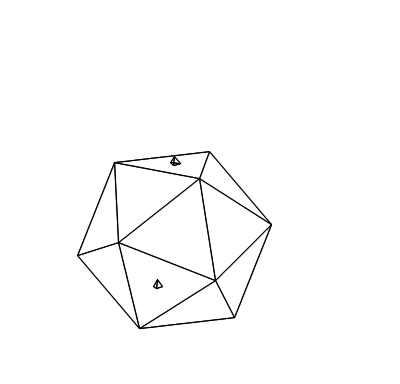
「算数・数学」の部屋に戻る