線対称の行列

ｙ＝ａｘ　(ａ≠０) 関して対称移動したときの表現行列を求めます。

ｙ＝ａｘ　(ａ≠０) に対して点Ａ（ｍ，ｎ）と
対象な点を考えると、点Ａを通り、ｙ＝ａｘ に垂直な直線は
　ｙ＝(-1/a)（ｘ−ｍ）＋ｎ
これと、ｙ＝ａｘ の交点は
　−ｘ／ａ＋ｍ／ａ＋ｎ＝ａｘ
より、
　−ｘ＋ｍ＋ａｎ＝ａ²ｘ
　ｘ＝(ｍ＋ａｎ)/(ａ²＋１)
このとき、
　ｙ＝ａ(ｍ＋ａｎ)/(ａ²＋１)
よって、移動先の点は、点Ａを、点（(ｍ＋ａｎ)/(ａ²＋１)，ａ(ｍ＋ａｎ)/(ａ²＋１)）に関して、
対象に移動させた点であるので、
　（２(ｍ＋ａｎ)/(ａ²＋１)−ｍ，２ａ(ｍ＋ａｎ)/(ａ²＋１)−ｎ）と書け、
求める行列は、

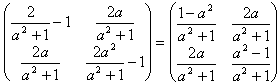
となります。


この行列をさらに分析すると、
ａ＝０　とした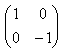は、ｘ軸対象の移動であるし、
ａ→∞ の極限である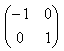は、y軸対象の移動である。
また、ａ＝１ としたときの、 は、ｙ＝ｘ に関する移動であり、よく知られている
線対称移動は、すべてこの形になる。

算数・数学の部屋に戻る